안녕하세요. 테크 랩에서 이미지 인식 기술 연구 개발을 하고 있는 Zhan(湛)입니다. 이번 글에서는 사내에서 진행하는 CPython 스터디에서 발표한 내용을 바탕으로 메모리 모델의 기초를 설명하겠습니다. Sequential Consistency(이하 SC)와 Total Store Order(이하 TSO)라는 두 가지 메모리 모델을 다룰 텐데요. 각 메모리 모델을 형식화해 이해하는 과정에서 스스로 메모리 모델에 대해 생각해 볼 수 있다면 좋겠습니다.
CPython 스터디를 시작한 계기와 PEP 703
메모리 모델에 대한 설명을 시작하기 전에 왜 CPython 스터디를 하게 되었는지, 어떤 계기로 이 주제를 발표하게 됐는지 설명하겠습니다. 이 장은 본론과 관련없는 내용이니 메모리 모델이 궁금해 들어오신 분이라면 바로 다음 장으로 건너가셔도 괜찮습니다.
저는 주 업무를 하고 있는 테크 랩이라는 조직 외에, 사내 Python 이용을 지원하는 조직인 Python 팀에도 소속돼 있습니다. Python 팀에서는 사내에서 CPython의 RPM 패키지를 빌드하거나 CI를 위해 Screwdriver.cd 템플릿을 제공하는 등의 활동을 하는데요. 몇 달 전부터 사내 Python 스킬 향상을 위해 'CPython 스터디'라는 Python 중급자 대상의 스터디 모임을 진행하고 있습니다.
이 글은 CPython 스터디에서 발표한 내용을 바탕으로 작성했습니다. PEP 703과 관련해 참조 카운트 구현을 읽다가 SEQ_CST와 RELAXED 등 메모리 모델 관련 키워드를 만났습니다(예: pyatomic_gcc.h). CPython 코드를 읽기 위해 메모리 모델를 꼭 이해해야 하는 것은 아니지만, 저 수준(low level) 코드를 읽다 보면 가끔씩 나오던 개념이라서 이번 기회에 공부해 봤습니다.
PEP 703에 대해서 조사한 것은 단순한 호기심 때문이기도 하지만, 주 업무인 딥 러닝에도 도움이 될 것이라고 생각했기 때문입니다. PEP 703의 Motivation 절에 나와 있듯 멀티 스레드로 확장하면 PyTorch의 DataLoader 성능 및 사용 편의성이 향상될 가능성이 있는데요. 이미지 관련 딥 러닝에서 데이터 로딩과 전처리에서 병목 현상이 발생하는 경우가 많기 때문에 PEP 703이 구현되면 꼭 업무로 검증해 보고 싶습니다.
SC는 명령이 작성된 순서대로 실행되는 프로그래머의 직관에 부합하는 모델입니다. 반면, x86이나 ARM, RISC-V와 같은 현대의 일반적인 CPU는 명령의 실행 순서를 바꿀 수 있다는 점에서 좀 더 느슨한 모델에 따라 작동합니다. 이번에 설명할 TSO는 x86 CPU의 동작을 형식화한 모델입니다(ARM이나 RISC-V는 TSO 보다 더 느슨한 모델(Relaxed Memory Consistency)을 따르고 있지만 여기서는 자세히 설명하지 않겠습니다).
글은 다음과 같은 순서로 진행됩니다.
- SC에서는 허용되지 않는 이상한 동작이 실제 CPU에서 발생하는 중요한 예시를 살펴보기
- 프로그래머의 직관에 부합하는 SC 형식화하기
- 실제 CPU에서 왜 SC에서 허용하지 않는 동작이 발생하는지 성능 관점에서 살펴보기
- TSO를 형식화해 x86 CPU의 메모리 모델 정확히 이해하기
- 고급 언어와 메모리 모델의 관계 보충 설명
이 글은 A Primer on Memory Consistency and Cache Coherence라는 책을 전반적으로 참고해 작성했으며, 인용한 부분에는 [1]과 함께 인용한 위치를 남겨 놓았습니다.
SC에서는 허용되지 않는 이상한 동작이 실제 CPU에서 발생하는 예시
다음 프로그램([1]의 표 3.3)을 '예시 1'이라고 합니다. 여기서 S1, S2는 저장 명령, L1, L2는 로드 명령입니다. x, y는 메모리 주소이고, r1, r2는 레지스터를 나타내는데요. 이 프로그램을 실행하면 r1과 r2의 값은 어떻게 될까요?
| 코어 C1 | 코어 C2 | 코멘트 |
|---|---|---|
| S1: x = NEW; | S2: y = NEW; | /* 초깃값은 x = 0 & y = 0 */ |
| L1: r1 = y; | L2: r2 = x; |
병렬 프로그램에는 비결정성이 있기 때문에 결과가 하나로 결정되지 않습니다. 몇 가지 패턴을 생각해 보면 r1, r2 = (NEW, NEW), (0, NEW), (NEW, 0)의 가능성이 있음을 알 수 있습니다.
- S1 < S2 < L1 < L2 → (NEW, NEW)
- S1 < L1 < S2 < L2 → (0, NEW)
- S2 < L2 < S1 < L1 → (NEW, 0)
그렇다면 r1, r2 = (0, 0)이라는 결과는 나올 수 있을까요? 조금 생각해 보면 그럴 것 같지 않습니다.
- r1 = 0으로 가정한다.
- 이때 L1 < S2이다.
- 각 코어의 프로그램 순서에 따라 S1 < L1, S2 < L2이다.
- 2번과 3번에 의해 S1 < L1 < S2 < L2와 같은 순서가 결정된다.
- S1 < L2이므로 r2 = NEW이다.
위와 같은 '소박한 추론'은 맞을까요? 하드웨어에 따라 다르다는 것이 정확한 답입니다. 예를 들어, MIPS R10000이라는 CPU에서는 맞지만, x86이나 ARM, RISC-V 등 현대의 일반적인 CPU에서는 잘못된 것입니다. 하드웨어에 따라 메모리 모델이 다르기 때문입니다(아래로 갈수록 느슨해짐).
- SC(Sequential Consistency): MIPS R10000
- TSO(Total Store Order): x86
- RC(Relaxed Consistency): ARM
r1, r2 = (0, 0)이라는 실행 결과를 허용하는 x86과 ARM의 동작은 언뜻 보기에 이상한데요. 이 글의 주제는 '이러한 동작을 어떻게 이해할 것인가'입니다.
SC 형식화
SC는 앞 절에서 전개한 '소박한 추론'을 형식화한 것입니다. 다음과 같이 정의를 설명합니다. 이는 [1]의 3.5절에서 설명한 것과 같습니다.
프로그램 순서(<p)와 메모리 순서(<m)라는 두 가지 순서를 도입한다. <p는 코어별 전체 순서이고 <m은 글로벌 전체 순서이다. 이 순서는 다음 두 가지 조건을 만족한다.
(1)각 코어의 프로그램 순서는 메모리 순서에 반영된다. 다음과 같이 네 가지 경우가 있다(여기서 a, b는 서로 같을 때와 그렇지 않을 때를 모두 포함함).
- If L(a) <p L(b) ⇒ L(a) <m L(b) /* Load → Load */
- If L(a) <p S(b) ⇒ L(a) <m S(b) /* Load → Store */
- If S(a) <p S(b) ⇒ S(a) <m S(b) /* Store → Store */
- If S(a) <p L(b) ⇒ S(a) <m L(b) /* Store → Load */
(2)주소 a에 대��한 로드 명령으로 얻은 값은 직전 주소 a에 대한 저장 명령으로 저장된 값이다.
- Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) }
다음 그림([1]의 그림 3.3)은 위 정의에 따라 앞서 살펴본 예시 1을 분석한 것입니다. 좌우 양 끝에 있는 아래쪽 화살표가 코어별 프로그램 순서(<p)를, 중앙에 있는 아래쪽 화살표가 글로벌 메모리 순서(<m)를 나타냅니다.
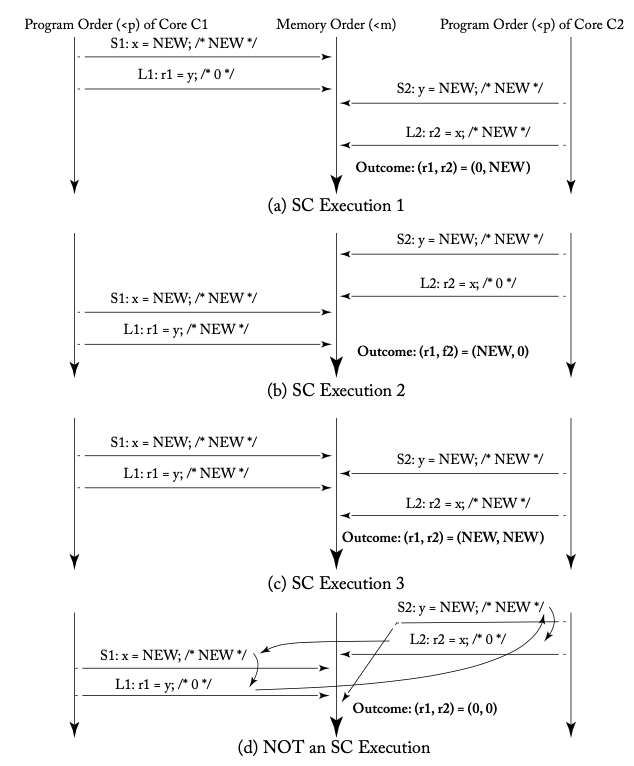
앞서 정의(1)에서 프로그램 순서는 메모리 순서에 반영되므로, 위 그림에서 a, b, c의 가로 방향 화살표는 교차되지 않고 직선으로 뻗어 있습니다. r1, r2 = (0, 0)이라는 실행 결과가 그림에서 d로 표시되어 있는데요. 이는 화살표가 교차돼 있기 때문에 SC의 정의에 어긋난다는 것을 알 수 있습니다.
이번에 한 프로그램 순서와 메모리 순서를 사용하여 'r1, r2 = (0, 0)이라는 실행 결과는 없다'는 앞 장의 논의를 다시 정리해 보겠습니다.
- r1 = 0으로 가정한다.
- 이때 정의(2)에 따라 L1 <m S2이다.
- 정의(1)에 따라 각 코어의 프로그램 순서 S1 <p L1, S2 <p L2는 메모리 순서에 반영되므로 S1 <m L1, S2 <m L2이다.
- 2번과 3번에 따라 S1 <m L1 <m L1 <m S2 <m L2라는 순서가 결정된다.
- S1 <m L2와 정의(2)에 따라 r2 = NEW이다.
이번 장에서 형식화한 SC는 직관적이고 다루기 쉬운 메모리 모델이지만, 실제 CPU가 해당 모델을 따르지 않는 이유는 성능 때문입니다. 다음 장에서는 이와 관련된 설명을 하겠습니다.
SC를 벗어나고 싶은 이유 - 저장 버퍼
TSO를 형식화하기 전에 왜 SC를 벗어나고 싶은지 그 이유를 설명하겠습니다. 현재의 CPU는 메모리 쓰기(저장) 지연을 감추기 위해 일반적으로 아래 그림([1]의 그림 4.4a)과 같이 각 코어가 저장 버퍼(store buffer)라는 영역을 갖고 있습니다.
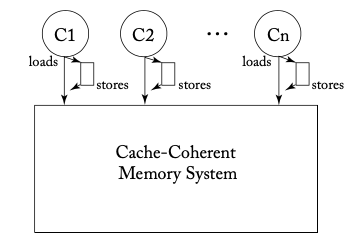
이 저장 버퍼를 가진 CPU가 첫 번째 예시 프로그램을 실행한다고 생각해 봅시다.
| 코어 C1 | 코어 C2 | 코멘트 |
|---|---|---|
| S1: x = NEW; | S2: y = NEW; | /* 초깃값은 x = 0 & y = 0 */ |
| L1: r1 = y; | L2: r2 = x; |
그러면 다음과 같은 실행 예시를 생각해 볼 수 있습니다.
- C1이 S1을 실행하고 S1이 버퍼에 들어간다.
- C2가 S2를 실행하고 S2가 버퍼에 들어간다.
- C1과 C2가 각각 L1과 L2를 실행한다(S1, S2는 아직 메모리에 반영되지 않았기 때문에 초깃값(0, 0)이 읽힌다).
- 버퍼에서 S1과 S2가 나와 반영된다.
위 예시 3에서 L1이 S1을, L2가 S2를 추월한다는 점에 주의해야 합니다. 이 현상을 메모리 접근 작업의 교체(reordering)라고 하며, 이를 시각화한 것이 아래 그림([1]의 그림 4.2d)입니다.
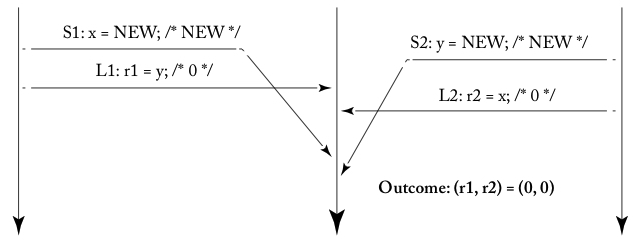
S1과 L1, S2와 L2의 선이 교차하는 것으로 보아 이 실행 예시가 SC를 만족하지 않는다는 것을 알 수 있습니다. 이런 이상한 실행 예시가 나타나지 않도록 하드웨어를 구현하는 방법도 생각해 볼 수 있지만, x86에서는 성능을 위해 이와 같은 작동을 허용했습니다.
참고로 위 예시는 멀티 코어에 관한 예시입니다. 싱글 코어의 경우 저장 버퍼를 투명하게 처리할 수 있습니다. 로드 명령을 실행할 때 메모리를 참조하기 전에 저장 버퍼를 들여다보면 아직 메모리에 반영되지 않은 저장 명령 값을 얻을 수 있기 때문입니다. 이를 바이패싱(bypassing)이라고 합니다.
이번 장에서는 메모리 접근 작업의 교체와 바이패싱이라는 두 가지 현상을 하드웨어 관점에서 설명했습니다. 다음 장에서는 이를 어떻게 수학적으로 형식화할 것인지 알아보겠습니다.
TSO 형식화
먼저 다음와 같이 TSO를 정의하겠습니다. SC와의 차이를 알 수 있는 부분에는 취소선을 사용해 표기했습니다. 이 정의는 [1]의 4.3절과 유사합니다. 이 글에서는 메모리 펜스(fence) 명령에 대한 설명은 생략합니다.
(1) 각 코어의 프로그램 순서는 메모리 순서에 반영된다. 다음과 같이 네 가지 경우가 있다.
- If L(a) <p L(b) ⇒ L(a) <m L(b) /* Load → Load */
- If L(a) <p S(b) ⇒ L(a) <m S(b) /* Load → Store */
- If S(a) <p S(b) ⇒ S(a) <m S(b) /* Store → Store */
- If S(a) <p L(b) ⇒ S(a) <m L(b) /* Store → Load */ /* 변경 사항 1: 저장 버퍼 도입 */
(2) 주소 a에 대한 로드 명령으로 얻은 �값은 직전 주소 a에 대한 저장 명령으로 저장된 값이다:
- Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) } /* 변경 사항 2: 바이패싱 고려 필요 */
- Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) 또는 S(a) <p L(a) }
위 정의(1)에서 Store → Load 교체가 허용된 결과, 예시 1에서 r1, r2 = (0, 0)이라는 실행 결과가 허용됩니다.
위 정의(2)를 이해하기 위해 다음 예시 2를 살펴보겠습니다.
| 코어 C1 | 코어 C2 | 코멘트 |
|---|---|---|
| S1: x = NEW; | S2: y = NEW; | /* 초깃값은 x = 0 & y = 0 */ |
| L1: r1 = x; | L2: r2 = y; | |
| L3: r3 = y; | L4: r4 = x; | /* r2 = 0 & r4 = 0으로 가정한다*/ |
이때 아래와 같은 실행 예시([1]의 그림 4.3)가 허용됩니다.
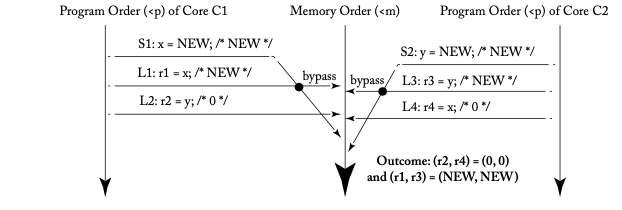
위 그림에서 메모리 순서로는 L1 <m S1이지만, 프로그램 순서로는 S1 <p L1이므로 L1은 S1의 값을 읽을 수 있습니다(바이패싱). 정의에 따라 L1의 값을 계산하고 이를 확인해 봅시다.
- 위 정의(2)에 따르면 L1의 값은 {S(x) | S(x) <m L1(x), 또는 S(x) <p L1(x)}라는 집합에서 얻을 수 있습니다.
- 이 집합을 계산하면 {S1}이 됩니다.
- 따라서 S1이 저장한 NEW가 L1의 값이 됩니다.
한편, SC의 정의에 따르면 L1의 값은 {S(x) | S(x) <m L1(x)}라는 집합에서 얻을 수 있는데요. 위 그림에서 L1보다 메모리 순서가 작은 명령은 없으므로 이는 공집합이 됩니다. 따라서 L1의 값은 초깃값인 0이 됩니다. 정의(2)를 변경함으로써 확실히 바이패싱 동작을 형식화할 수 있음을 알 수 있습니다.
고급 언어에서 메모리 모델을 의식할 필요가 있을까?
고급 언어 프로그래밍을 할 때 메모리 모델을 의식할 필요가 있을까요? 대답은 기본적으로 '없다'입니다. 이는 "SC for DRF programs(sequential consistency for data race free programs)"라는 문구로 알려져 있습니다. 두 개 이상의 스레드가 동기화 작업 없이 동일한 메모리 주소에 접근할 때 그 중 쓰기 작업이 있는 경우 이를 데이터 경합이라고 하는데요(더 엄밀한 정의는 [1]의 5.4절을 참조). 프로그래머는 잠금(lock) 등을 적절히 사용해 데이터 경합이 발생하지 않도록 프로그래밍해서 SC적인 실행을 기대할 수 있습니다.
예를 들어, Java 사양(Java Language Specification, JLS)에는 다음과 같이 나와 있습니다(JLS 17.4.3).
If a program has no data races, then all executions of the program will appear to be sequentially consistent.
C++와 같은 언어도 원자적(atomic) 연산이 아닌 잠금으로 동기화하는 프로그래밍을 하는 한 SC로 간주할 수 있습니다(A Memory Model for C++: Sequential Consistency for Race-Free Programs).
Here we argue that programs which are data-race-free by the definitions in the strawman proposal, and do not use atomic operations, behave according to sequential consistency rules.
여기서 JLS의 "the program will appear to be sequentially consistent"라는 표현에 주목해 봅시다. 프로그램이 정말로 SC로 실행되는지가 아니라 그렇게 보이는(appear to be) 것이 중요합니다. 즉, '메모리 접근 순서가 뒤바뀐다는 것'과 '그것을 관찰할 수 있다는 것'은 별개의 문제인 것입니다.
예를 들어, 아래 예시([1]의 그림 5.7)는 변수의 레지스터 할당이라는 컴파일러의 최적화로 메모리 접근 순서가 뒤바뀌는 것을 나타냅니다. 해당 변수 A의 값을 관측하는 다른 스레드가 없다면 해당 최적화는 SC로 간주할 수 있습니다.
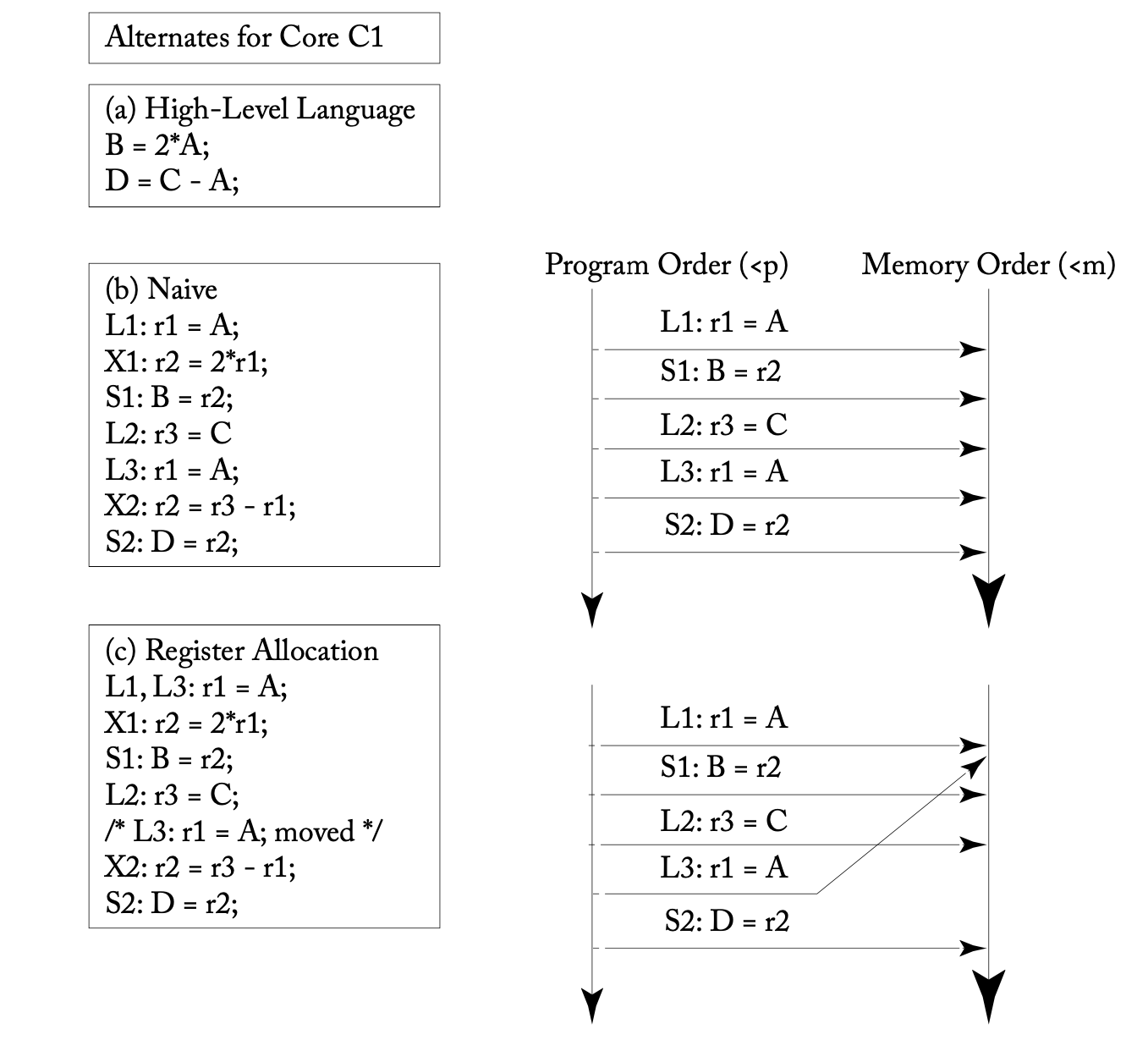
다만, '고급 언어 프로그래머는 기본적으로 SC를 기대할 수 있다'는 주장에는 예외가 존재합니다. 예를 들어 C, C++, Rust, Java와 같은 언어에는 메모리 순서를 지정할 수 있는 원자적 연산이 있습니다(C++, Rust, Java). SC에 해당하는 메모리 순서를 지정하는 한 문제가 없지만, 더 느슨한 메모리 순서를 지정하는 경우에는 그에 해당하는 메모리 모델을 꼭 이해해야 합니다.
또한, 기계어를 생성하는 프로그램을 작성하는 컴파일러 엔지니어와 같은 프로그래머도 메모리 모델을 이해해야 합니다. 멀티 스레드 소스 코드에 대해 프로세서별 메모리 모델에 따라 적절한 메모리 펜스 명령을 출력해야 하기 때문입니다.
참고 문헌
더 깊이 공부하고 싶은 분들을 위해 몇 가지 참고 문헌을 소개합니다.
[1] A Primer on Memory Consistency and Cache Coherence
[2] プログラマーのためのCPU入門 ― CPUは如何にしてソフトウェアを高速に実行するか(프로그래머를 위한 CPU 입문)
[3] Rust Atomics and Locks
[4] C++ Concurrency in Action
이 글을 작성하면서 『A Primer on Memory Consistency and Cache Coherence』를 전면적으로 참고했습니다. 이 글에서는 메모리 모델에 대한 설명에 그쳤지만, 해당 책에서는 메모리 모델과 캐시 일관성의 관계도 다루고 있습니다. 오픈 액세스로 이용할 수 있으니 꼭 읽어보시기 바랍니다.
『プログラマーのためのCPU入門 ― CPUは如何にしてソフトウェアを高速に実行するか』(프로그래머를 위한 CPU 입문)에서는 프로그램 속도 향상이라는 관점에서 CPU의 다양한 측면을 배울 수 있습니다. 이 글과 관련된 내용은 10장부터 12장에 걸쳐서 나와 있습니다. 이번에는 메모리 액세스 순서가 뒤바뀌는 원인으로 저장 버퍼에 대해 설명했지만, 해당 책의 11.2절에서는 다른 요인에 대해서도 다루고 있습니다.
원자적 연산을 이용한 프로그래밍을 하고자 한다면 『Rust Atomics and Locks』와 『C++ Concurrency in Action』이 좋은 입문서가 될 것입니다. 고급 언어와 메모리 모델의 관계에 대해 이 글에서는 'SC for DRF programs'라는 개념의 개요를 소개하는데 그쳤는데요. 많은 프로그래머들은 잠금이나 큐와 같은 높은 수준의 부품을 사용해 프로그래밍하는 것으로 충분하겠지만, CPython의 참조 카운트 예시처럼 속도를 높이기 위해 원자적 연산을 직접 사용하는 경우에는 이와 같은 지식이 중요할 수 있습니다.