メモリモデル入門（Sequential ConsistencyとTotal Store Orderを理解する）

LINEヤフー Advent Calendar 2023の16日目の記事です。

こんにちは。テックラボで画像認識技術の研究開発を担当している湛です。

社内で開催しているCPython勉強会での発表を元にメモリモデルの初歩を解説します。
本記事ではSequential Consistency（SC）とTotal Store Order（TSO）という2つのメモリモデルを取り上げます。フォーマルな定義に基づいてメモリモデルを理解することにより、自分で手を動かしてメモリモデルについて考えられるようになることを目指します。

背景（CPython勉強会とPEP 703）

メモリモデルの解説に入る前に、なぜCPython勉強会を開催しているのか、またどのようなきっかけでこのテーマについて発表しようと思ったかについて説明します。本論とは関係ないのでこの節は飛ばしてもらっても大丈夫です。

私は主務のテックラボとは別に社内のPython利用のサポートを行うチームにも所属しています。Pythonチームでは社内向けにCPythonのRPMパッケージをビルドしたり、CIのためにScrewdriver.cdのテンプレートを提供していたりします。他の活動としては社内のPythonスキル向上のため、数ヶ月前からCPython勉強会というPython中級者向けの勉強会を開催しています。

本記事はCPython勉強会での発表が元になっています。PEP 703に関連して参照カウントの実装を読んでいたところ、SEQ_CSTやRELAXEDなど、メモリモデルに関係するキーワードが出てきました（たとえばpyatomic_gcc.h）。CPythonの実装を読むためにメモリモデルの理解は必須ではありません。しかし低レイヤーのコードを読んでいるとたまに出てくる概念なので、この機会に少し腰を据えて勉強しました。

PEP 703について調査していたのは単純な興味もあるのですが、本業の深層学習にも役立ちそうだという考えがあります。PEP 703のMotivationという節にあるように、マルスレッドがスケールするようになると、PyTorchのDataLoaderの性能や使いやすさが向上する可能性があります。画像系の深層学習において、データのロードや前処理がボトルネックになることはよくあるので、PEP 703が実装されたらぜひ業務で検証したいと考えています。

SCは命令が書かれた順番通り実行されるような、プログラマーの直感に合うモデルです。一方でx86やARMやRISC-Vのような現代の一般的なCPUは命令の実行順序の入れ替えを許容するという意味でより緩いモデルに従って動作しています。今回解説するTSOはx86 CPUの動作を定式化したモデルです。ARMやRISC-VはTSOよりさらに緩いモデル（Relaxed Memory Consistency）に従っているのですが、今回は詳しく解説しません。

構成は以下の通りです。

第1節ではまず重要な例をひとつ紹介します。この例においてはSCでは許されないような不思議な挙動が現実のCPUで発生します。
第2節では次にプログラマーの直感に合うSCを形式化します。
そして第3節ではなぜ現実のCPUにおいてSCが破れるかをパフォーマンスの観点から解説します。
第4節ではTSOの形式化を行い、x86 CPUのメモリモデルを厳密に理解できるようになります。
最後に第5節で高級言語とメモリモデルの関係について補足します。

また本記事は全体を通してA Primer on Memory Consistency and Cache Coherenceという教科書を参考にしています。以下ではこの資料を[1]という表記で引用します。

まずは例から

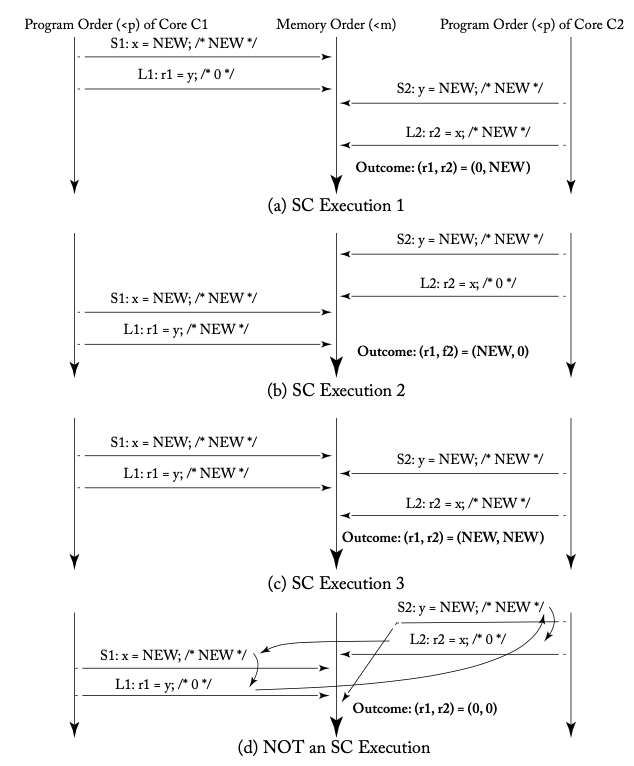
以下のプログラム（[1]の表3.3）を例1とします。これを実行したとき、r1, r2の値はどうなっているでしょうか？　ここでS1, S2はストア命令、L1, L2はロード命令です。そしてx, yはメモリアドレス、r1, r2はレジスタを表しています。

コアC1	コアC2	コメント
S1: x = NEW;	S2: y = NEW;	/* 初期値は x = 0 & y = 0 */
L1: r1 = y;	L2: r2 = x;

並列プログラムには非決定性があるので、結果はひとつには決まりません。いくつかパターンを考えてみると、 r1, r2 = (NEW, NEW), (0, NEW), (NEW, 0) の可能性があることがわかります:

S1 < S2 < L1 < L2 → (NEW, NEW)
S1 < L1 < S2 < L2 → (0, NEW)
S2 < L2 < S1 < L1 → (NEW, 0)

では r1, r2 = (0, 0) という結果はありうるでしょうか？少し考えてみるとこれはなさそうに思えます：

r1 = 0を仮定する
このときL1 < S2である
各コアのプログラムの順序よりS1 < L1, S2 < L2である
2と3よりS1 < L1 < S2 < L2という順序が決定される
S1 < L2よりr2 = NEWである

以上の「素朴な推論」は正しいでしょうか？ハードウェアによるというのが正確な答えです。たとえばMIPS R10000というCPUでは正しいですが、x86やARMやRISC-Vなど現代の一般的なCPUでは誤りです。これはハードウェアによってメモリモデルが異なるからです（下に行くほど緩い）:

Sequential Consistency (SC): MIPS R10000
Total Store Order (TSO): x86
Relaxed: ARM

r1, r2 = (0, 0) という実行結果を許容するx86やARMの挙動は、一見不思議です。本記事のテーマは、これらの挙動をどう理解するかです。

Sequential Consistencyの形式化

SCは、前節で展開したような「素朴な推論」を形式化したものです。以下に定義を述べます。これは[1]の3.5節で述べられているものと同じです。

プログラム順序（<p）とメモリ順序（<m）という2つの順序を導入する。<pはコアごとの全順序で<mはグローバルな全順序である。これらの順序は以下の2条件を満たす。

（1）各コアのプログラム順序はメモリ順序に反映される。以下の4つのケースがある（ここでa, bは互いに等しい場合もそうでない場合も含む）：

If L(a) <p L(b) ⇒ L(a) <m L(b) /* Load → Load */
If L(a) <p S(b) ⇒ L(a) <m S(b) /* Load → Store */
If S(a) <p S(b) ⇒ S(a) <m S(b) /* Store → Store */
If S(a) <p L(b) ⇒ S(a) <m L(b) /* Store → Load */

（2）アドレスaに対するロード命令から得られる値は、直前のアドレスaに対するストア命令で保存された値である：

Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) }

下の図（[1]の図3.3）は、以上の定義によって例1を分析したものです。左右両端にある下向き矢印がコアごとのプログラム順序（<p）で、中心にある下向き矢印がグローバルなメモリ順序（<m）を表しています。

定義（1）よりプログラム順序はメモリ順序に反映されるので、図中のa, b, cの横向きの矢印は交差せずにまっすぐ伸びています。r1, r2 = (0, 0) という実行結果が図中のdで示されていますが、これは矢印が交差しているのでSCの定義に反していることがわかります。

今回導入したプログラム順序とメモリ順序を使って「r1, r2 = (0, 0)という実行結果はない」という前節の議論を書き直してみます：

r1 = 0を仮定する
このとき定義（2）よりL1 <m S2である
定義（1）より各コアのプログラム順序S1 <p L1, S2 <p L2はメモリ順序に反映されるのでS1 <m L1, S2 <m L2である
2と3よりS1 <m L1 <m S2 <m L2という順序が決定される
S1 <m L2と定義（2）よりr2 = NEWである

今節で定式化したSCは、直感的で扱いやすいメモリモデルです。にもかかわらず現実のCPUがこのモデルに従っていないのは、パフォーマンスが理由です。次の節では、そのあたりの事情を解説します。

Sequential Consistencyを破りたくなる理由：ストアバッファ

TSOの形式化をする前に、なぜSCを破りたくなるかという理由を説明します。現代のCPUではメモリ書き込み（ストア）のレイテンシーを隠すために、下図（[1]の図4.4a）のように各コアがストアバッファという領域を持つのが一般的です。

このストアバッファを持ったCPUが、最初の例に挙げたプログラムを実行することを考えてみましょう。

コアC1	コアC2	コメント
S1: x = NEW;	S2: y = NEW;	/* 初期値は x = 0 & y = 0 */
L1: r1 = y;	L2: r2 = x;

すると、以下のような実行例が考えられます：

C1がS1を実行し、S1がバッファに入る
C2がS2を実行し、S2がバッファに入る
C1とC2がそれぞれL1とL2を実行する（S1, S2はまだメモリ反映されていないので初期値 (0, 0) が読まれる）
バッファからS1とS2が取り出されて、反映される

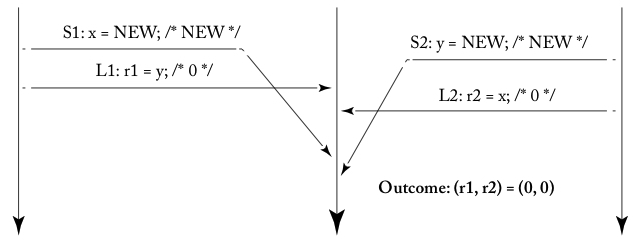
3においてL1がS1を（そしてL2がS2を）追い越していることに注意してください。この現象をメモリアクセス操作の入れ替え（reorder）と言います。そしてこれを可視化したものが、以下の図（[1]の図4.2d）です。S1とL1およびS2とL2の線が交差していることから、この実行例がSCを満たしていないことがわかります。

このような変な実行例が現れないように、ハードウェアを実装するというやり方も考えられます。しかしx86ではパフォーマンスのために、このような実行例を許容しました。

以上の例はマルチコアについてでしたが、シングルコアの場合はストアバッファは透過的に扱えます。ロード命令を実行するとき、メモリを参照する前にストアバッファのなかをのぞくことで、メモリにまだ反映されていないストア命令の値を取得できるからです。この挙動をbypassingと呼びます。

今節ではメモリアクセス操作の入れ替えと、bypassingという2つの現象をハードウェアの視点から解説しました。次の節では、これをどう数学的に形式化するかという問題に取り組みます。

Total Store Orderの形式化

以下のようにTSOを定義します。またSCとの差分がわかるように、打ち消し線を使って表記します。この定義[1]の4.3節と同様のものです。本記事では、メモリフェンス命令については省略しています。

（1）各コアのプログラム順序はメモリ順序に反映される。以下の4つのケースがある。

If L(a) <p L(b) ⇒ L(a) <m L(b) /* Load → Load */
If L(a) <p S(b) ⇒ L(a) <m S(b) /* Load → Store */
If S(a) <p S(b) ⇒ S(a) <m S(b) /* Store → Store */
~~If S(a) <p L(b) ⇒ S(a) <m L(b) /* Store → Load */~~ /* 変更点1：ストアバッファの導入 */

（2）アドレスaに対するロード命令から得られる値は、直前のアドレスaに対するストア命令で保存された値である：

~~Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) }~~ /* 変更点2：bypassingの考慮が必要 */

Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) または S(a) <p L(a) }

上の定義（1）においてStore → Loadの入れ替えが許された結果、例1について r1, r2 = (0, 0) という実行結果が許容されます。

定義の（2）について理解するために、以下の例2を考えてみましょう。

コアC1	コアC2	コメント
S1: x = NEW;	S2: y = NEW;	/* 初期値は x = 0 & y = 0 */
L1: r1 = x;	L2: r2 = y;
L3: r3 = y;	L4: r4 = x;	/* r2 = 0 & r4 = 0 を仮定する*/

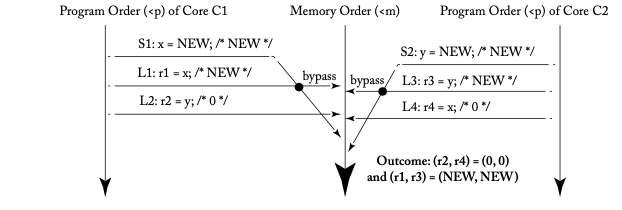
このとき、以下のような実行例（[1]の図4.3）が許容されます。

上の図においてメモリオーダーとしてはL1 <m S1ですが、プログラムオーダーにおいてS1 <p L1なので、L1はS1の値を読めます（bypassing）。定義に従ってL1の値を計算し、これを確認してみましょう。

上の定義（2）によると、L1の値は{S(x) | S(x) <m L1(x) 、または S(x) <p L1(x)}という集合から得られます。この集合を計算すると {S1} になります。したがって、S1がストアしたNEWがL1の値になります。

一方で、SCの定義ではL1の値は{S(x) | S(x) <m L1(x)}という集合から得られます。しかし上図においてL1よりメモリ順序が小さい命令はないので、これは空集合になります。従ってL1の値は、初期値である0になってしまいます。定義（2）を変更したことによって、たしかにbyppasingの挙動が定式化できていることがわかります。

高水準言語とメモリモデル

高水準言語のプログラミングをするときに、メモリモデルを意識する必要はあるでしょうか？　基本的にはないというのが回答です。これはSC for DRF programs （Sequential Consistency for Data Race Free programs）というフレーズで知られています。2つ以上のスレッドが同期操作なしに同じメモリアドレスにアクセスし、そのなかに書き込み操作があった場合を、データ競合と言います（より厳密な定義は[1]の5.4節を参照してください）。
したがってプログラマーはロックなどを適切に使い、データ競合が発生しないようにプログラミングすることで、SCな実行を期待できるというわけです。

たとえばJavaの仕様（Java Language Specification, JLS）には以下のように書いてあります（JLS 17.4.3）:

If a program has no data races, then all executions of the program will appear to be sequentially consistent.

C++のような言語についてもアトミック操作ではなく、ロックで同期するようなプログラミングをしている限りでは、SCと見なせます（A Memory Model for C++: Sequential Consistency for Race-Free Programs）

Here we argue that programs which are data-race-free by the definitions in the strawman proposal, and do not use atomic operations, behave according to sequential consistency rules.

さて、JLSの “the program will appear to be sequentially consistent” という表現に注目しましょう。プログラムが本当にSCに実行されているかどうかではなく、そのように見える（appear to be）ことが重要です。すなわちメモリアクセス順序の入れ替えが起きていることと、それを観測できることは別です。
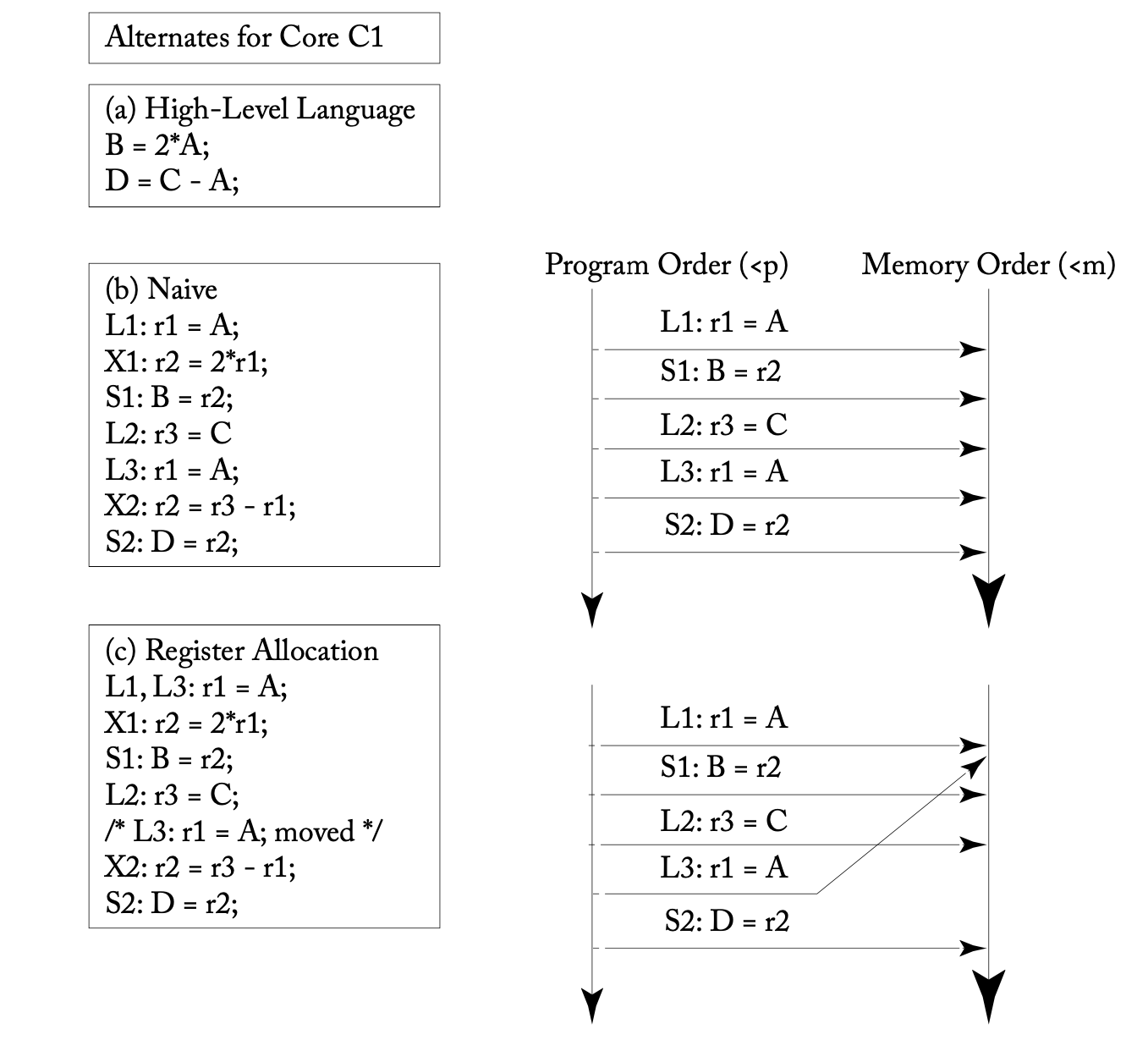
たとえば以下の例（[1]の図5.7）は、変数のレジスタ割り付けというコンパイラによる最適化がメモリアクセス順序の入れ替えることを示しています。この変数Aの値を観測する別のスレッドがなければ、この最適化はSCと見なせるのです。

高水準言語のプログラマーは基本的にSCを期待できるという主張には例外が存在します。C, C++, Rust, Javaなどの言語にはメモリオーダーを指定できるアトミック操作があります（C++、Rust、Java）。SCに相当するメモリオーダーを指定している限りは問題ありませんが、より緩いメモリオーダーを指定する場合にはそれに対応するメモリモデルの理解が不可欠です。

また、機械語を生成するプログラムを書くコンパイラエンジニアのようなプログラマーもメモリモデルに対する理解が必要です。マルチスレッドのソースコードに対して、プロセッサごとのメモリモデルに応じて適切なメモリフェンス命令を出力する必要があります。

参考文献案内

さらに学びを深めたい方のために、いくつかの参考文献を紹介します。

[1] A Primer on Memory Consistency and Cache Coherence（外部サイト）
[2] プログラマーのためのCPU入門（外部サイト）
[3] 詳解 Rustアトミック操作とロック（外部サイト）
[4] C++ Concurrency in Action（外部サイト）

本記事の執筆に際し、全面的に参考にしたのが『A Primer on Memory Consistency and Cache Coherence』です。今回はメモリモデルの解説にとどまっていますが、この本ではメモリモデルとキャッシュコヒーレンシーの関係についても論じられています。オープンアクセスで利用可能なので、ぜひ読んでみてください。

『プログラマーのためのCPU入門』では、プログラムの高速化という視点からCPUのさまざまな側面を学べます。本記事に関連する内容は、第10章から第12章にわたって記載されています。今回はメモリアクセスの順序が入れ替わる原因としてストアバッファについて解説しましたが、この本の11.2節では他の要因についても触れられています。

アトミック操作を使ったプログラミングをするなら、『詳解 Rustアトミック操作とロック』や『C++ Concurrency in Action』が良い入門書です。高級言語とメモリモデルの関係について、本記事では「SC for DRF programs」という考え方の概要を紹介するに留めました。
多くのプログラマーにとっては、ロックやキューなどの高レベルな部品を使ってプログラミングするので十分です。CPythonの参照カウントの例のように、高速化のためにアトミック操作を直接使う場合にはこのような知識が重要となるでしょう。