Hello, I'm Zhan(湛) from the Technology Incubation Division. I work in research and development of image recognition technology. In this post, I'll explain the basics of memory models, drawing from a presentation I gave at a CPython study session within our company. We'll explore two memory models: sequential consistency (SC) and total store order (TSO). My goal is to help you understand these concepts better and encourage you to reason about memory models with formal models.
Why I started the CPython study and PEP 703
Before delving into memory models, let me share why I initiated the CPython study and chose this topic for my presentation. If you're here mainly for the memory models, feel free to skip ahead to the next section, as this part isn't directly related to the core topic.
Besides my main role at the Technology Incubation Division, I'm also involved with the company's Python team, which supports internal Python usage. The Python team's activities include building CPython RPM packages and providing Screwdriver.cd templates for continuous integration (CI). A few months ago, we launched a study group aimed at helping intermediate Python users within the company enhance their skills.
This article is based on what I presented at the CPython study. While exploring the implementation of reference counting in relation to PEP 703, I came across terms related to memory models, like SEQ_CST and RELAXED (see pyatomic_gcc.h for example). Although not crucial for reading CPython code, these concepts often appear in low-level code, prompting me to delve deeper into the subject.
My investigation into PEP 703 was sparked by curiosity, but I also believed it could aid my main work in deep learning. As outlined in the Motivation section of PEP 703, expanding to use multi-threading has the potential to enhance both performance and usability of PyTorch's DataLoader. This is especially relevant in image-based deep learning, where bottlenecks in data loading and preprocessing are common. If PEP 703 is implemented, I'm eager to put it to the test in my professional tasks.
Sequential consistency (SC) is a model that matches the programmer's expectation that instructions will execute in the order they were written in. On the other hand, modern CPUs like x86, ARM, and RISC-V follow a more relaxed model that allows for reordering of command execution. The total store order (TSO) model, which I'll discuss, formalizes the behavior of x86 CPUs. While ARM and RISC-V adhere to an even more relaxed model known as relaxed memory consistency, I won't delve into that here.
The article will follow this outline:
- Exploring a crucial example of unusual behavior that SC does not permit but which actually occurs in real CPUs
- Formalizing SC as an introduction to a formalization of memory models
- Investigating why real CPUs exhibit behaviors that SC does not allow, from a performance standpoint
- Formalizing TSO to gain a precise understanding of the x86 CPU memory model
- Further explaining the connection between high-level languages and memory models
This article draws extensively from the book A Primer on Memory Consistency and Cache Coherence, and I have indicated citations with [1] and included the specific locations referenced.
An example of unusual behavior not permitted in SC that occurs in actual CPUs
Consider the following program (Table 3.3 from [1]), which we'll call "Example 1". In this example, S1 and S2 are store instructions, while L1 and L2 are load instructions. The variables x and y are memory addresses, and r1 and r2 are registers. What would be the values of r1 and r2 after running this program?
| Core C1 | Core C2 | Comments |
|---|---|---|
| S1: x = NEW; | S2: y = NEW; | /* Initial values: x = 0 & y = 0 */ |
| L1: r1 = y; | L2: r2 = x; |
Because parallel programs contain nondeterminism, the results are not confined to one definite outcome. By contemplating various patterns, we can identify that there are possibilities for the values of r1 and r2 to be (NEW, NEW), (0, NEW), or (NEW, 0).
- S1 < S2 < L1 < L2 → (NEW, NEW)
- S1 < L1 < S2 < L2 → (0, NEW)
- S2 < L2 < S1 < L1 → (NEW, 0)
So, is it possible to get a result where r1, r2 = (0, 0)? Upon further thought, it seems unlikely. Consider the following reasoning:
- Assume r1 = 0.
- In this case, L1 executes before S2.
- According to the program order on each core, S1 executes before L1, and S2 executes before L2.
- Based on points 2 and 3, we determine the sequence: S1 before L1 before S2 before L2.
- Given that S1 executes before L2, the result must be r2 = NEW.
Is this kind of "naive reasoning" accurate? The exact answer varies with the hardware. For instance, while this reasoning would hold true for a CPU like the MIPS R10000, it would not apply to contemporary common CPUs such as x86, ARM, or RISC-V. This discrepancy is due to the different memory models adopted by various hardware architectures, which tend to become more relaxed further down the hierarchy.
- Sequential consistency: MIPS R10000
- Total store order: x86
- Relaxed consistency: ARM
The behavior of x86 and ARM architectures, which permits an execution result of r1, r2 = (0, 0), may seem counterintuitive at first glance. The main topic of this article is "how to interpret such behavior".
Formalizing SC
SC formalizes the "naive reasoning" outlined in the previous section. The definition is as follows, consistent with Section 3.5 in [1]:
We introduce two kinds of orderings: program order (<p) and memory order (<m). <p represents the total order within each core, while <m is the global total order. These orders must satisfy the following conditions:
(1) The program order of each core is reflected in the memory order. There are four possible scenarios (where a and b may be the same or different):
- If L(a) <p L(b) ⇒ L(a) <m L(b) /* Load → Load */
- If L(a) <p S(b) ⇒ L(a) <m S(b) /* Load → Store */
- If S(a) <p S(b) ⇒ S(a) <m S(b) /* Store → Store */
- If S(a) <p L(b) ⇒ S(a) <m L(b) /* Store → Load */
(2) The value retrieved by a load instruction for address a must be the value that was last stored by a store instruction for that same address a.
- Value of L(a) = Value of MAX<m {S(a) | S(a) <m L(a) }
The following diagram (Figure 3.3 from [1]) analyzes Example 1, previously discussed, based on the definition provided. The downward arrows on the far left and right represent the program order (<p) for each core, and the central downward arrow indicates the global memory order (<m).
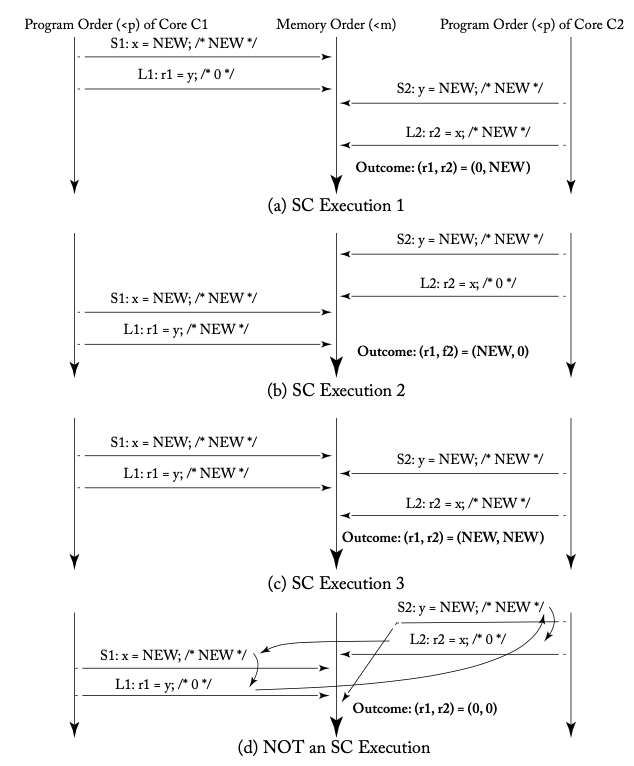
As previously defined, the program order is reflected in the memory order, so in the diagram above, the horizontal arrows labeled a, b, and c are depicted as straight lines without crossing. The execution result r1, r2 = (0, 0) is marked as d in the diagram, which shows that such a result, indicated by crossing arrows, contradicts the definition of SC.
Now, let's revisit the discussion from the previous section using program and memory orders to clarify why the result r1, r2 = (0, 0) isn't possible.
- Let's assume r1 = 0.
- By definition (2), this means L1 <m S2.
- According to definition (1), the program orders S1 <p L1 and S2 <p L2 for each core are mirrored in the memory order, resulting in S1 <m L1 and S2 <m L2.
- Combining points 2 and 3, we deduce the sequence: S1 <m L1 <m S2 <m L2.
- With S1 <m L2 and in line with definition (2), it follows that r2 = NEW.
The SC model formalized in this chapter is intuitive and straightforward. However, real CPUs don't follow this model, mainly for performance reasons. We'll explore this further in the next chapter.
Why we want to move beyond SC - The role of store buffers
Before we formalize TSO, let's discuss why there's a need to move beyond SC. To hide the latency of memory writes (stores), modern CPUs generally equip each core with a region known as a store buffer, as illustrated below (Figure 4.4a from [1]).
Imagine a CPU with store buffers running the first example program.
| Core C1 | Core C2 | Comments |
|---|---|---|
| S1: x = NEW; | S2: y = NEW; | /* Initial values: x = 0 & y = 0 */ |
| L1: r1 = y; | L2: r2 = x; |
This scenario could unfold as follows:
- Core C1 executes S1. S1 is then placed in the buffer.
- Core C2 executes S2. S2 also goes into the buffer.
- C1 and C2 execute L1 and L2, respectively (since S1 and S2 haven't yet been committed to memory, the initial values 0, 0 are read).
- The buffered S1 and S2 are eventually committed to memory.
In the third step of the example above, it's important to note that L1 overtakes S1, and L2 overtakes S2. This phenomenon is referred to as the reordering of memory access operations, and it's visualized in the diagram below (Figure 4.2d from [1]).
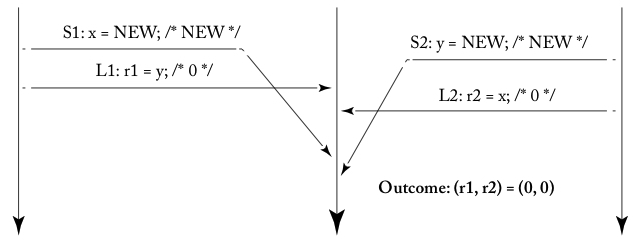
The crossing lines between S1 and L1, and S2 and L2, indicate that this execution example does not comply with SC. While it is feasible to design hardware that prevents such atypical execution scenarios, x86 has chosen to permit this behavior to enhance performance.
For context, the example given relates to multi-core processors. In a single-core scenario, the store buffer can be handled in a way that is transparent to the program. This is because executing a load instruction involves checking the store buffer before accessing memory, allowing the program to retrieve the value from a store instruction that hasn't yet been committed to memory. This mechanism is known as bypassing.
This chapter has described two hardware-related phenomena: reordering of memory access operations and bypassing. Next, we'll look at how these can be formalized mathematically.
Formalizing TSO
Let's begin by defining TSO. To highlight the differences from SC, I've used strikethroughs on the parts that differ. This definition closely resembles Section 4.3 in [1]. Please note, this article omits details about memory fence (fence) instructions.
(1) The program order of each core is reflected in the memory order. Here are the four scenarios:
- If L(a) <p L(b) then L(a) <m L(b) /* Load to Load */
- If L(a) <p S(b) then L(a) <m S(b) /* Load to Store */
- If S(a) <p S(b) then S(a) <m S(b) /* Store to Store */
- If S(a) <p L(b) then S(a) <m L(b) /* Store to Load */ /* Change 1: Introduction of store buffers */
(2) The value retrieved by a load instruction for address a is the value that was last stored by a store instruction for that same address a:
- Value of L(a) = Value of MAX <m {S(a) | S(a) <m L(a) } /* Change 2: Bypassing needs to be considered */
- Value of L(a) = Value of MAX <m {S(a) | S(a) <m L(a) } or S(a) <p L(a)
According to definition (1), which permits the reordering of Store to Load, the execution result of r1, r2 = (0, 0) in Example 1 is allowed.
To understand definition (2) better, let's look at Example 2:
| Core C1 | Core C2 | Comments |
|---|---|---|
| S1: x = NEW; | S2: y = NEW; | /* Initial values: x = 0 & y = 0 */ |
| L1: r1 = x; | L2: r2 = y; | |
| L3: r3 = y; | L4: r4 = x; | /* Assume r2 = 0 & r4 = 0 */ |
In this situation, the execution scenario depicted in Figure 4.3 from [1] is permissible.
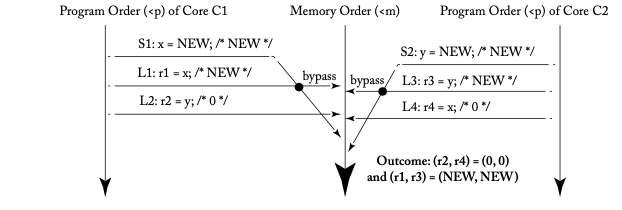
In the diagram, although L1 comes after S1 in memory order (<m), the program order (<p) is S1 before L1, which allows L1 to read the value from S1 (bypassing). Let's calculate the value of L1 according to the definition and check the result.
- Per the revised definition (2), the value of L1 is obtained from the set {S(x) | S(x) <m L1(x) or S(x) <p L1(x)}.
- Calculating this set results in {S1}.
- Therefore, the value that S1 stores, which is NEW, is the value read by L1.
On the other hand, under SC's definition, the value of L1 would be derived from the set {S(x) | S(x) <m L1(x)}. In the diagram, there are no instructions preceding L1 in memory order, so this set would be empty. Consequently, the value of L1 would default to the initial value, which is 0. By altering definition (2), we can clearly formalize the concept of bypassing.
Should we be mindful of memory models in high-level language programming?
Is there a need to consider memory models when programming in high-level languages? Generally, the answer is "no". This concept is encapsulated in the phrase "sequential consistency for data race-free (DRF) programs". A data race occurs when two or more threads access the same memory address without synchronization, and at least one of the threads performs a write operation (for a more rigorous definition, refer to Section 5.4 in [1]). By properly using locks or other synchronization constructs to prevent data races, programmers can expect SC-like behavior in their programs.
For instance, the Java Language Specification (JLS) states the following (JLS 17.4.3):
If a program has no data races, then all executions of the program will appear to be sequentially consistent.
Similarly, languages like C++ consider programs that synchronize using locks (as opposed to atomic operations) to be sequentially consistent, as long as they are free of data races (A Memory Model for C++: Sequential Consistency for Race-Free Programs).
Here we argue that programs which are data-race-free by the definitions in the strawman proposal, and do not use atomic operations, behave according to sequential consistency rules.
Let's note the wording used by JLS: "the program will appear to be sequentially consistent." The emphasis is not on whether the program actually executes in SC fashion, but rather that it appears to be SC. This distinction highlights that "the reordering of memory accesses" and "the ability to observe such reordering" are separate issues.
For instance, the optimization scenario depicted below (Figure 5.7 from [1]), which involves variable register allocation by the compiler, demonstrates how the order of memory accesses can be changed. If no other thread is observing the value of variable A, then this optimization can be regarded as SC.
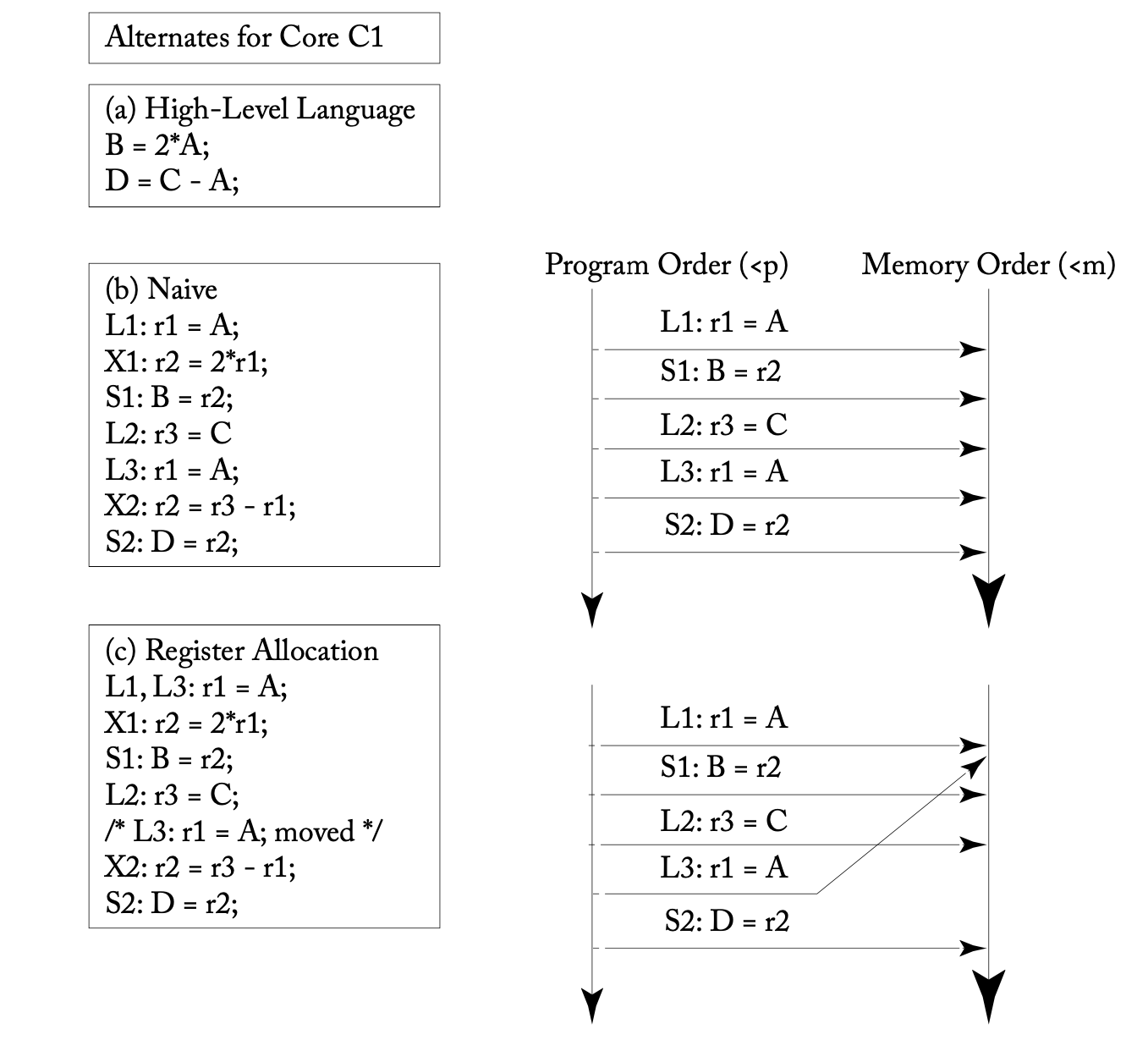
However, there are exceptions to the assertion that "high-level language programmers can generally expect SC". Languages such as C, C++, Rust, and Java provide atomic operations with specified memory ordering (C++, Rust, Java). While there's no problem as long as the memory order corresponding to SC is used, understanding the relevant memory model becomes essential when opting for a more relaxed memory order.
Moreover, programmers such as compiler engineers, who create programs that generate assembly code, need to comprehend memory models as well. They are responsible for emitting the correct memory fence instructions in accordance with the processor's memory model when dealing with multi-threaded source code.
References
For those interested in delving deeper, here are some recommended readings:
[1] A Primer on Memory Consistency and Cache Coherence
[2] プログラマーのためのCPU入門 ― CPUは如何にしてソフトウェアを高速に実行するか(Introduction to CPU for Programmers)
[3] Rust Atomics and Locks
[4] C++ Concurrency in Action
While writing this article, I extensively referenced "A Primer on Memory Consistency and Cache Coherence". This article focused on explaining memory models, but the book also covers the relationship between memory models and cache coherence. It's available for open access, so I highly recommend reading it.
"プログラマーのためのCPU入門 ― CPUは如何にしてソフトウェアを高速に実行するか" provides insights into various aspects of CPUs from the perspective of improving program speed. The content related to this article is covered from Chapters 10 to 12. While this article explained store buffers as a reason for the reordering of memory access, Section 11.2 of the book also discusses other factors.
If you're interested in programming with atomic operations, "Rust Atomics and Locks" and "C++ Concurrency in Action" would serve as excellent introductions. This article only gave an overview of the concept of "SC for DRF programs" in relation to high-level languages and memory models. While many programmers may find it sufficient to use high-level constructs like locks or queues, the knowledge of memory models becomes important when directly using atomic operations to increase speed, as in the case with CPython's reference counting.