Yahoo!広告ディスプレイ広告におけるABテスト実践：デルタ法、AAテストシミュレーション、検出力分析の自動化

導入

こんにちは、LINEヤフーの広告プロダクトのサイエンス部に所属している高橋、鈴木、中村です。新しい施策をプロダクトに導入する際、皆さんはどのようにその効果を評価していますか？多くの場合、一部の本番トラフィックに対して施策を適用し、施策を適用しなかったトラフィックとの性能の差分を測定するABテストが広く実施されていると思います。今回は、Yahoo!広告のディスプレイ広告（YDA）におけるABテストを支える技術をご紹介します。

ABテストの直面する課題

ABテストは、サービスのトラフィックをグループに分け、一方に新しい施策を導入してその効果を評価する手法です。施策を導入しないグループをコントロールバケット（対照群）、施策を導入するグループをテストバケット（比較群）と呼びます。ABテストの実施にはいくつかの課題があります。

• 実験単位に基づく有意差検定: ABテストでは、施策の効果を正確に評価するために、実験単位に基づいた有意差検定が必要です。注目するメトリクスについて、適切な分布への収束定理を適用することで、検定を保証する理論的背景が整います。

• テストの正当性確保: 外れ値やサンプル数不足によりテスト結果の信頼性が損なわれる可能性があります。テストの仮定を十分満たしていることを評価することは、テスト結果から誤った示唆を得ることを防ぎます。

• 事前のテスト計画: テストから有意義な結果を得るために必要なトラフィック量を事前に知りたいケースがあります。有意な効果を検出するためのトラフィック量を算出することで、テストのリソースを適切に配分できます。

• 迅速な結果解釈の必要性: 多くの施策をトライアンドエラーで検証する場合、迅速な結果解釈が求められます。ABテストにまつわる分析を自動化することで、次の意思決定に素早く繋げられるとともに分析の正確性を高めます。

これらの課題を解決するための技術は、YDAにおけるABテストを支え、効果的かつ効率的な施策実施を可能にします。本記事では、それら技術の詳細をご紹介していきます。

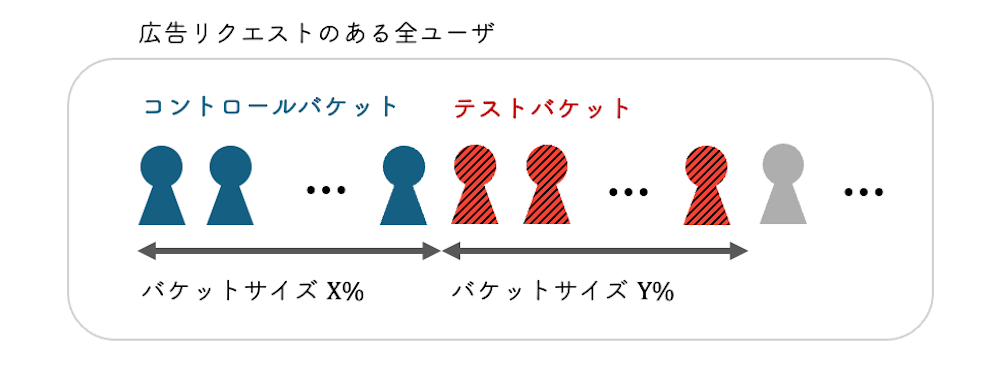
YDAにおけるバケット分割

YDAにおけるABテストは、効果的な施策評価を行うために、広告リクエスト（トラフィック）をユーザー単位で分割しています。これにより、各ユーザーは一貫した広告配信の体験を維持したまま、特定の施策に対してのみ影響されます。このユーザー単位での分割を行うことで、外部要因による変動を最小限に抑え、施策による影響をより正確に評価できます。

コントロールバケットとテストバケットへの振り分けは、バケットサイズと呼ばれる割合を調整することで制御します。バケットサイズは、特定の施策をどれほどのユーザーに対して適用するかを制御する値であり、全体のユーザー母集団に対する割合として設定されます。これにより、異なる施策の影響を検証するためのリソース配分や、ビジネス上のリスクを考慮したテスト設計が可能になります。

有意差検定 - デルタ法による信頼区間の算出 -

ここではコントロールバケットとテストバケットで得られた結果を比較し、統計的仮説検定をすることを考えます。なお、上記のバケット分割においてユーザー間は独立であると想定します。

例としてどちらのバケットで広告のクリック率（CTR）が高かったか比較をしたいとします。このときリクエストを1標本としたt検定を実施することが思いつきますが、今回のケースでこれは不適当です。これは実験単位がユーザーであり、同一ユーザーのリクエスト間でユーザー内の相関があることが見込まれるためです。

そこでユーザーを1標本とみなし、ユーザー単位でクリック数やリクエスト数を集約します。そしてこのユーザー単位の値の標本平均から全体のCTRを表現し直すことができると、デルタ法（delta method）という定理によりCTRが正規分布に分布収束し、その平均と分散を推定できることが示されます。具体的には、期間内でのユーザー $i$ ($i=1, ..., n$) のリクエスト数 $R_i$ とクリック数 $C_i$、およびその標本平均 $\overline{R}$、 $\overline{C}$ に対し、全体のCTRは $\overline{C}/\overline{R}$ として表現できます。そして $(R_1, ..., R_n)$ や $(C_1, ..., C_n)$ はユーザーごとにi.i.d.と仮定すると、 $\overline{R}$、 $\overline{C}$ は中心極限定理により $n \to \infty$ でそれぞれ正規分布に分布収束します。そしてその2変量の比として定義されるCTRもまた正規分布に分布収束し、その平均と分散は $R_i$ や $C_i$ の平均と分散から算出できることがデルタ法により示されます（詳細は後述します）。すなわちユーザー単位のリクエスト数とクリック数の統計量を集計することで、CTRが漸近する正規分布の近似が計算できます。

こうして得られた正規分布を用いれば、各バケットの信頼区間の計算やバケット間の差の検定をCTRについて実施できます。コントロールバケットとテストバケットでのCTRの正規分布の近似が $\mathcal N(\hat \mu_{\mathrm{CTRL}}, \hat \sigma^2_{\mathrm{CTRL}})$、 $\mathcal N(\hat \mu_{\mathrm{TEST}}, \hat \sigma^2_{\mathrm{TEST}})$ として得られたとき、あらかじめ決めていた有意水準に対応する正規分布の上側 $\alpha$% 点を $z_\alpha$ として、帰無仮説 $\mu_{\mathrm{TEST}} - \mu_{\mathrm{CTRL}} = 0$ に対する両側検定の採択域を $0 \pm z_{\alpha} \sqrt{\hat \sigma^2_{\mathrm{CTRL}} + \hat \sigma^2_{\mathrm{TEST}}}$ と算出することができ、 $\hat \mu_{\mathrm{TEST}} - \hat \mu_{\mathrm{CTRL}}$ がこの棄却域の外にあればCTRが有意に高い（低い）と主張できます。

以上で、我々のシステムにおける信頼区間および差の検定の算出方法の主なロジックについて説明しました。なお説明のためにCTRを分析対象としましたが、広告で主要なKPIとなりうる下記のメトリクスについて同様に成り立ちます。

• CPC（Cost Per Click）: クリック単価
• RPR（Revenue Per Request）: リクエスト単価
• CVR（Conversion Rate）: コンバージョン率
• CPA（Cost Per Action）: コンバージョン単価

有意差検定の可視化について

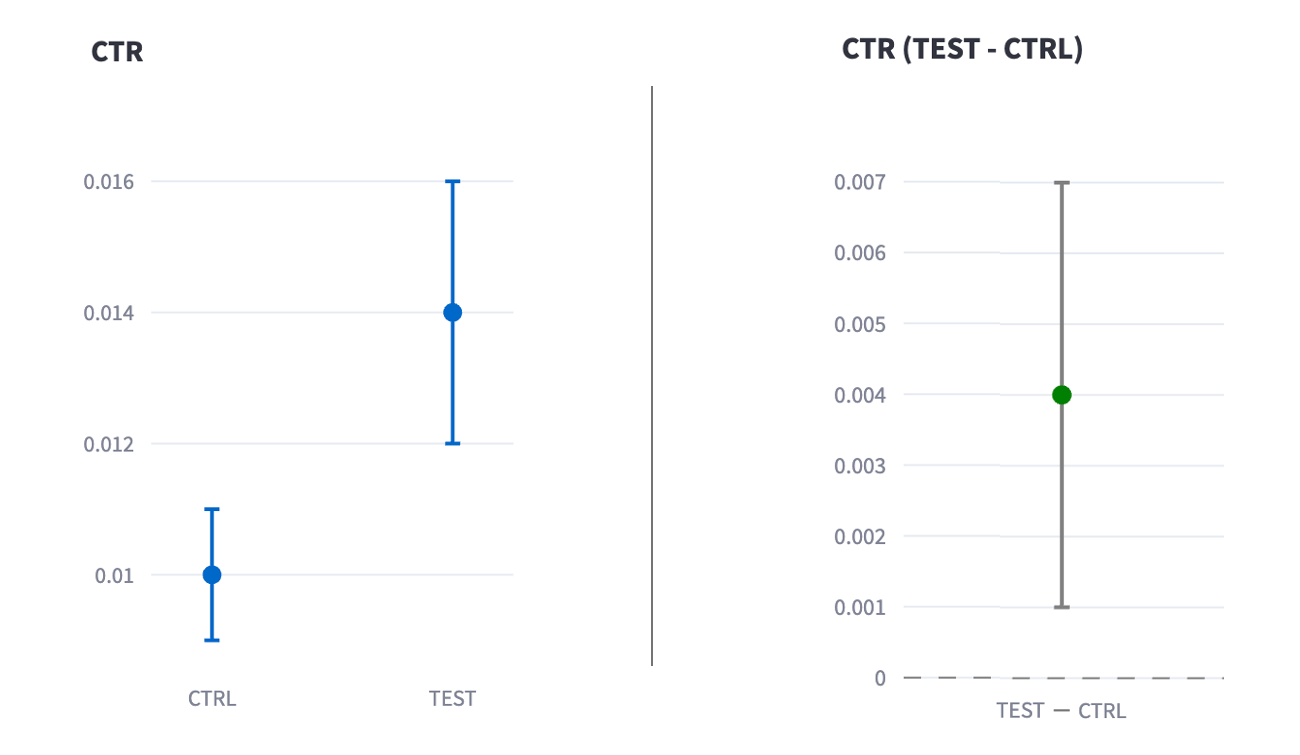
我々のシステムでは、ユーザー単位のメトリクスを定常集計し、指定したバケットについて統計量を集計することで、いくつかのメトリクスに対する信頼区間や差の検定の結果を表示するツールを作成しています。下図は可視化ツールでの表示のイメージです（数値はダミーのものを使用しています）。

左図は各バケットのCTRとその信頼区間を図示しています。縦軸はCTRの値、横軸はバケットを示し、マーカーがCTRの標本値、区間表示が信頼区間を意味します。右図はバケット間のCTRの差とその信頼区間を図示しています。縦軸はCTRの差の値、横軸はバケットを示し、マーカーが標本値の差、区間表示が差の信頼区間を意味します。なお、各信頼区間の有意水準はパラメーターとして与えられます。実験者は、差の信頼区間の下限が0を超えていることから、CTRLバケットと比較してTESTバケットでCTRが有意に増加していると判断できます。

補足: デルタ法について

ここではデルタ法の詳細について補足します[2, 3]。

$i$ ($i=1, ..., n$) に対してi.i.d.である確率変数 $\boldsymbol{\theta} _ i = \binom{\theta_{1, i}}{\theta_{2, i}}$ と、その標本平均 $\boldsymbol{\overline{\theta}} = \binom{\overline{\theta_{1}}}{\overline{\theta_{2}}}$ を考えます。$\boldsymbol{\overline{\theta}}$ は中心極限定理により $n \to \infty$ で正規分布に分布収束します。 $\boldsymbol{\theta} _ i$ の平均を $\boldsymbol{\mu}$、 $\boldsymbol{\theta} _ i$ の分散共分散行列を $\Sigma$ とすれば、以下のように表されます。

$\sqrt{n}(\boldsymbol{\overline{\theta}} - \boldsymbol{\mu} ) \xrightarrow{d} \mathcal N(\boldsymbol{0}, \Sigma)$

このような状況で、ある変数変換を施した $g(\boldsymbol{\overline{\theta}})$ の分布について考えたいとき、デルタ法が用いられます。デルタ法は、分布収束する確率変数の列に対し、連続微分可能な変数変換を施した確率変数についても分布収束することを示した定理です。特に上記のような正規分布に分布収束する $\boldsymbol{\overline{\theta}}$ と連続微分可能な変数変換 $g$ に対しては以下が成り立ちます。

$\sqrt{n} \left( g(\boldsymbol{\overline{\theta}}) - g(\boldsymbol{\mu}) \right) \xrightarrow{d} \mathcal N (\boldsymbol{0}, \nabla g (\boldsymbol{\mu})^{\top} \Sigma \nabla g (\boldsymbol{\mu}))$

これを先述のCTRのケースに当てはめると、 $i$ をユーザーとし、 $\theta_{1,i} = C_i$、 $\theta_{2,i} = R_i$ と対応付けられます。CTRは「クリック数÷リクエスト数」であるため、 $g(\boldsymbol{\overline{\theta}}) = \overline{\theta_{1}} / \overline{\theta_{2}}$ とし、CTR が以下のような正規分布 $\mathcal N(\mu, \sigma^2)$ に分布収束することが示されます。

$\begin{aligned} \mu &= \frac{\mu_1}{\mu_2} \\ \sigma^2 &= \frac{1}{N} \left(\frac{\mu_1}{\mu_2}\right)^2\left(\frac{\Sigma_{11}}{{\mu_1}^2} + \frac{\Sigma_{22}}{{\mu_2}^2} - \frac{2 \Sigma_{12} }{\mu_1 \mu_2}\right) \end{aligned}$

AAテストシミュレーション - テストの信頼性検証 -

前節ではデルタ法を利用した検定手法を紹介しましたが、これには正規分布への十分な収束という重要な仮定があり、これが成り立たない場合は有効な示唆を得られません。特に、デルタ法ではサンプル数不足や外れ値の存在によって正規性の近似仮定が崩れる可能性があります。

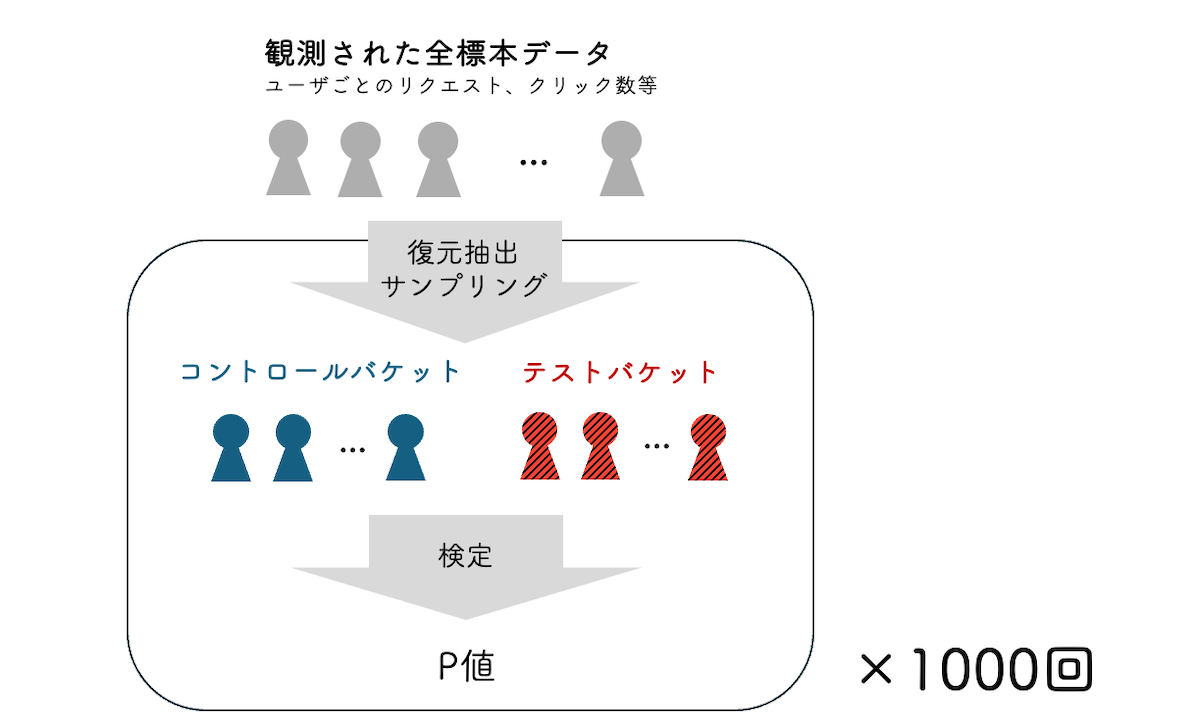
AAテストシミュレーションは、実施するテストや検定手法の信頼性を検証するための有効な手法です。この手法では、AAテスト（つまりバケット間で施策効果の差がない状況）において繰り返し検定結果を評価することで、検定の挙動に異常がないかをチェックできます。

シミュレーションでは、観測された全標本データを用います。観測された標本からランダムに2つのバケットを作成し、このバケット間の検定結果のP値を記録する操作を繰り返します。バケットは復元抽出サンプリングにより作成され、このときのシード値は繰り返しのたびに変更されます。シード値を都度変更することで毎回異なるバケットで検定を行うことになり、1回の検定では得られないP値の経験分布を得られます。テスト手法に問題がない場合、得られたP値は一様分布に従うことが知られており、逆に一様性を満たさない場合は、テスト手法になんらかの問題があることを示します[1]。

我々のシミュレーションでは、頻繁に設定されるテスト期間でユーザー単位の標本データを作成した上で、複数のバケットサイズにおけるシミュレーションを実施します。シミュレーションの試行回数は1000回とし、P値が一様分布に従うかを適合度検定で検証します。得られたP値の分布が一様分布には従わない場合には、デルタ法による検定結果を信頼しないことを推奨しています。

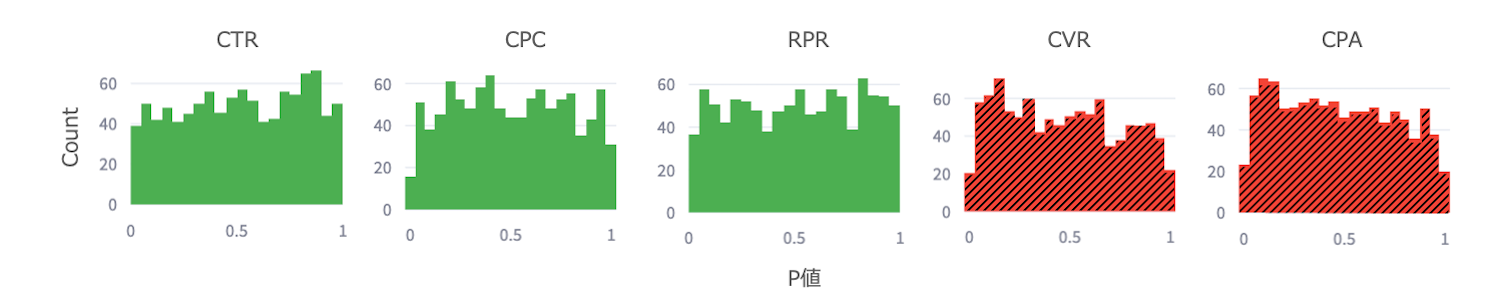
我々はこのAAテストシミュレーションを継続的に実施する仕組みを構築しており、各種KPIの検定結果の信頼性を評価しています。下図はYDAの主要なKPIにおけるP値のヒストグラムです。AAテストシミュレーションより得られる1000個のP値から経験分布を描いており、これよりP値の一様性を評価します。適合度検定（Kolmogorov-Smirnov検定）で一様性の仮説を棄却された場合を赤色斜線で、棄却されなかった場合を緑色無地で示しています。CTR、CPC、RPRは一様性を満たす一方で、CVR、CPAは満たしておらず、これらのKPIに対するデルタ法の検定結果は信頼できない可能性があります。

P値の一様性が満たされなかったとしても、検定を諦めることはありません。サンプル数を十分に確保するために、バケットサイズを拡大したりテスト期間を延長することで、必要な仮定を満たす可能性があります。我々の実験でも、バケットサイズを大きくすることでP値が一様性を満たしやすくなることを確認しています。この際、多重検定を考慮する必要がありますが、ここでは割愛します。

以上のように、AAテストシミュレーションでテストの信頼性を定期的に検証することで、テストから誤った示唆を得るリスクを低減しています。AAテストシミュレーションによるテストの信頼性検証は、弊社の検索モデリングに関するブログ記事でもご紹介がありますので、ぜひご覧ください。A/Bテストで想定外の結果が出たら？検定多重性の影響を定量的に分析する

検出力分析 - バケットサイズの計画 -

ABテストを行う際に、効果的な検出を保証するためには、テスト開始前にバケットサイズを計画することが大切です。施策の検証コストの制約で大きなバケットサイズを設定できない一方、小さすぎるとリリースに必要な施策の効果量を検出できないリスクもあります。この問題に対処するため、事前の検出力分析が役立ちます。

検出力とは、真に効果が存在する時に、それを有意に検出する確率を表します。バケットサイズを適切に計画するためには、まず有意水準（通常は5%）、期待する効果量、そして目標とする検出力（例: 80%）を設定する必要があります。これにより、適切なバケットサイズを算出できます。

以下の図は、CTRリフトの効果量（リフト率）と検出力の関係（Power curve）を、2つのバケットサイズ（X%とY%、ただしX>Y）に対して示しています。有意水準は5%とします。なお、この結果はYDAを模したダミーデータを用いており、実際のYDAテストがこの検出力と一致するわけではありません。

仮に、今回のテストで1.0%のCTRリフトを検出したいとします。Y%のバケットを用いる場合は、検出力は図より40%弱と低く、テストを実施しても効果を検出できない可能性が高いです。一方で、X%のバケットを用いる場合は、検出力は80%を超えており、十分な検出力が得られることがわかります。この結果より、このテストではX%のバケットサイズを設定することが望ましいと判断できます。

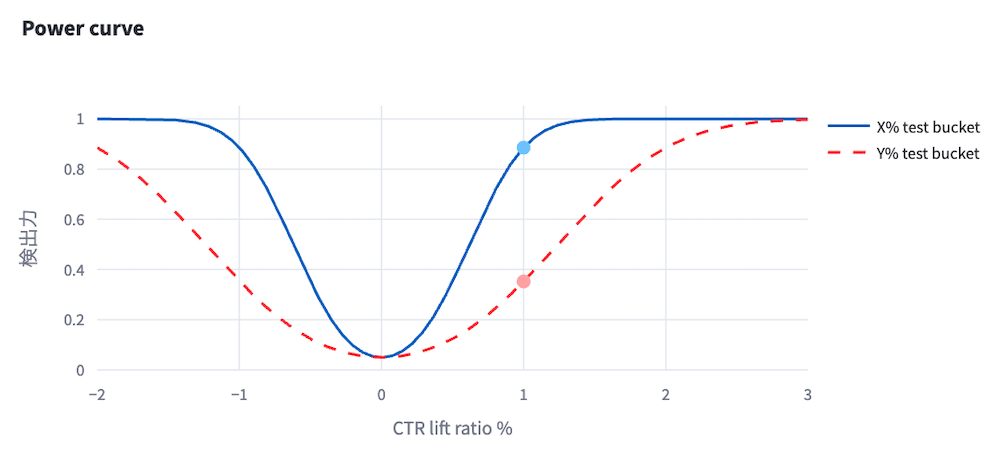
検出力の可視化は、事前にテストでどの程度のKPIリフトを検出できるかを予測し、必要なバケットサイズを計画するために有用です。しかし、事前の検出力分析はあくまでテストを実施する前のデータに基づく理論的な値であり、実際のテストではさまざまな要因（例えばテストロジックによるメトリクス分散の変化）によって検出力が変化する可能性もあります。バケットサイズの計画ではこれらのリスクに注意を払うことも重要です。

自動化による効率化

多くの施策をトライアンドエラーで繰り返し評価する現場では、迅速にテスト結果を分析し、次の施策に活かす必要があります。そのため、我々は信頼区間算出とAAテストシミュレーション、検出力分析を、リアルタイムのトラフィックデータを利用して自動的に可視化するシステムを構築しております。

このシステムはユーザー粒度での定常的な集計結果をテーブル化し、Streamlitを使用して最新の分析結果を可視化します。これにより、これまで手動だったデータ集計や検定処理の作業を、自動化されたシステムを通じて即座に実施でき、テスト計画や分析に必要な時間を大幅に短縮できるようになりました。

さらに、この自動化の取り組みは、効率向上に加え、テスト結果の信頼性を高める役割も果たしています。システムは設定された有意水準に基づき、信頼区間や検定結果を自動算出することで、計算ミスを排除し、一貫性のある結果を提供します。この一貫した結果により、迅速かつ正確な意思決定が可能になります。

おわりに

本記事では、ABテストの分析を支える技術についてご紹介し、YDAの中でどのように活用されているかの実例をご紹介しました。

サービスは大きくなればなるほど施策の数も増え、テストをサポートする技術の重要性は増していきます。今回ご紹介した技術が読者の皆さまに少しでもお役に立ちましたら光栄です。

参考文献

• [1] R. Kohavi, D. Tang, Y. Xu著, 大杉直也訳 (2021). A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは. ドワンゴ.
• [2] 久保川達也著 (2017). 現代数理統計学の基礎. 共立出版.
• [3] Alex Deng, Ulf Knoblich, Jiannan Lu (2018). Applying the Delta method in metric analytics: A practical guide with novel ideas. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.