はじめに
初めまして、LINE株式会社(現LINEヤフー株式会社)の2023年夏のインターンに参加させていただいた、東京大学大学院経済学研究科経済専攻経済学コース修士1��年の櫻井一郎です。
インターン期間中はCommerce Data Scienceチームに所属し、LINEギフトのデータを扱った分析をさせていただきました。
本レポートではその中で、今までLINEギフトというサービスを一度も使ったことがない人がLINEギフトを受け取ることでサービスを利用し始めるのか、またどのような要因がそれを決定づけるのかという分析についてお話しします。
背景・動機
皆さんはLINEギフトというサービスを使用されたことがありますか?
実は私は今回インターンでLINEギフトのチームに配属されるまで、一度もLINEギフトを使用したことがありませんでした。インターン入社初日に初めてギフト担当のDSチームに配属されることを聞き、一度も使ったことがないのに大丈夫かなと思ったのを覚えています。分析をするのだから一度は使ったほうが良いのではと思い、インターン期間中、何度かギフトを送ってみることにしました。いわば私はLINEのインターンに参加したことがきっかけでサービスを使い始めたわけです。
私のようなケースはとてもレアケースでしょう。では、一般的にどのようなことがきっかけとなり、ユーザーはサービスを使い始めるのでしょうか? ここにギフトというサービスの特殊性があると考えています。一般的に、何らかのサービスの利用者を増やそうと考えた際、運営側は広告を打ったり、クーポンを配ったりすると思います。そして、ユーザー側はそれをきっかけにサービスを使い始めたり、使い始めなかったりするでしょう。しかし、ギフトにはもう��一つ重要なきっかけがあります。それは自分がギフトを受け取ることです。ギフトという事業はユーザー同士が影響し合う可能性のある事業であり、自分がギフトを受け取ったことがきっかけで、そのサービスの存在や利便性を知り、使ってみようかなと思うようになることが考えられます。
今回、LINEギフトを分析するにあたって、私はこの点に着目しました。LINEギフトはユーザー間で双方向のつながりがあるサービスであり、かつ双方向のギフトの贈り合いが事業として収入になるサービスです。ギフトを受け取った人がどういった行動をするかは、サービスを分析していく上で重要な観点なのではないだろうかと考えました。そして、それを分析する際に以下の二つの視点があると考えました。
一つ目は、例えば、クーポン等の配布による効果を検証しようとした時に、クーポン利用による直接的な使用増加とクーポン利用による間接的な効果(クーポン使用後における更なる使用)に加えて、ギフトを受け取った人がその後サービスを利用するかという視点も重要だと考えられるため、どのギフトの受け取りによって、どのくらいのギフトの使用が誘起されたかを検証することです。
二つ目はLINEギフトで取り扱う商品について考える際や、クーポン等配信の際にも具体的にどういった配信が最も効率的にサービス利用者を増やすのに繋がるのかを考える際に有用な分析を行うことです。
インターン期間中の前半は一つ目に関する分析を行い、後半は二つ目に関する分析を行いました。本レポートでは、後者について扱います。
設計
LINEギフトの�受け取りが、新規ユーザーの使用にどのような影響を与えるか推定するため、以下のような回帰分析を行います。以下ではギフトを受け取った人を「Receiver」、贈った人を「Sender」とします。
データについて
2020/12/01 ~ 2021/11/30まで(2021年12月に大幅な欠損が生じているため)で、「今までLINEギフトを贈ったことも受け取ったこともない状態で、ギフトを初めて受け取った人」を抽出。ただし、ReceiverとSenderが共に日本のユーザーであるものに限ります。計算資源等の制約上、300,000件をランダムサンプリングして用います。また、変数がひとつでも欠損しているものは使用されていません。
変数
被説明変数
- 受け取り後370日間でReceiverがギフトを贈った際の金額の合計を対数変換したもの()
- 受け取り後370日間でReceiverがギフトを贈るかどうか(金額が0かどうか)
※誕生日(365日間隔)の利用が多いサービスであるため、370日間の利用状況を観察します
説明変数
Numericalな変数には全て対数変換()しており、それ以外のカテゴリカルな変数はダミー変数化しています。
- Sender & Receiverの属性
- LINEで互いに友達追加している友達の人数の総数
- 居住地(MLによる推定値)
- 性別(MLによる推定値)
- 年齢(MLによる推定値)
- 職業(MLによる推定値)
- 初めて受け取った商品の属性
- 商品カテゴリ
- 単価
- eギフトか配送ギフトか
- 直近2週間のその商品の購入数
- 直近2週間のその商品のPV数
- Senderがクーポンを使用したか
- Receiverの誕生日であるか
- Receiverの誕生日公開しているか
- 上記2つの変数の交差項
- 初めて受け取った日が何月であるか
- 初めて受け取った日のLINEギフトのプラットフォーム全体の受注金額合計
モデル
以下の3つのモデルを考えます。
- OLS
- IV(2SLS)
- Logit
IV推定では、内生変数を商品カテゴリとし、操作変数としてSenderが2019/01/01~2022/12/31にどのカテゴリの商品をそれぞれ何個贈ったかを用います(その観測自体は除く)。理由としては、Receiverの趣味嗜好がその後のReceiverの購入に影響を持つ恐れがあるためで、Receiverの属性とは独立であるが、SenderがReceiverに何をあげるかには相関しそうなSenderのカテゴリごとの購入履歴を操作変数として用いています。
なお、Heteroskedasticity-robust standard errorを使用し、OLSとIVではHC3を、LogitではHC1をそれぞれ用います。
分析
基礎統計
以下では主要な統計量のみを図示します(ランダムサンプリング後)。
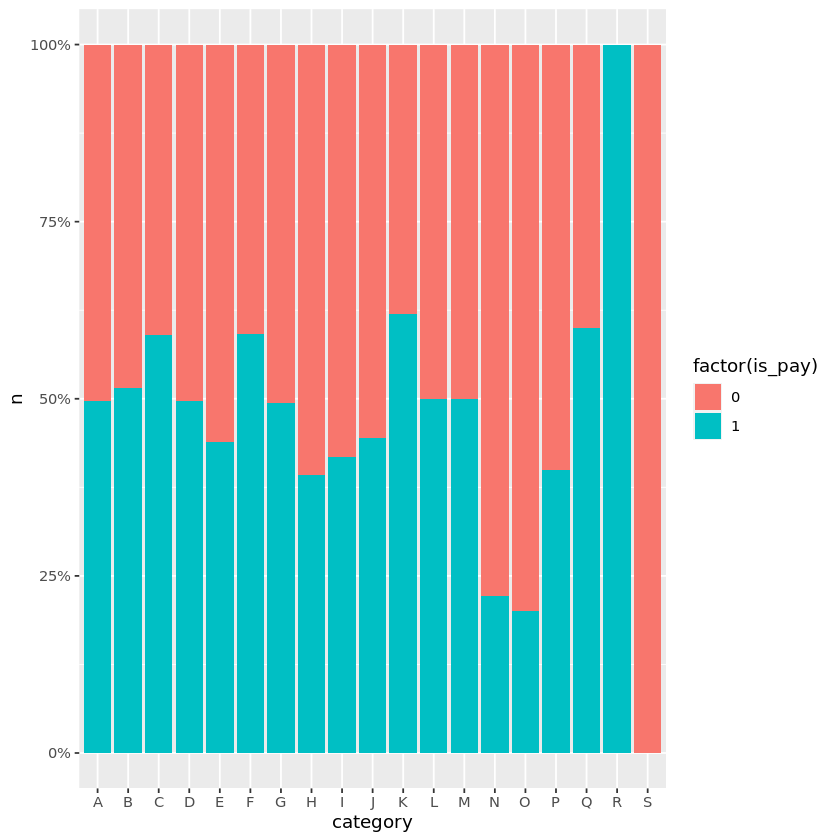
商品カテゴリごとの、その後の購入の分布
期間中に送られたギフトの各商品カテゴリについて、その後370日間でLINEギフトを贈ったReceiverの割合を表しています。
商品カテゴリごとの、その後の購入金額の常用対数の分布
期間中に送られたギフトの各商品カテゴリについて、その後370日間におけるReceiverの購入金額の対数値()の分布を表しています。
分析結果
以下では特に、Receiverの属性(居住地を除く)と商品のカテゴリについて見ていきます。ダミー変数の詳細な説明は以下のとおりです。また、単純化のために、結果の一部のみを表示しています。
|
ダミー変数
|
ベースグループ
|
ベースグループ以外
|
|---|---|---|
| r_sex | m:male | f:female |
| r_age | -14 | 15-19, 20-24, 25-29, 30-34, 35-39, 40-44, 45-49, 50- |
| r_occupation | 0: ある特定の職業 |
1-10: ベースグループ以外の職業10分類 ※本ブログでは情報割愛 |
| category_ | A: あるカテゴリ |
B-S: ベースグループ以外のカテゴリ18分類 ※本ブログでは情報割愛 |
表1-1:被説明変数が金額の合計(商品カテゴリ)
|
OLS
|
IV
|
OLS2
|
IV2
| |
|---|---|---|---|---|
| category_B | 0.177 (0.102)+ | 14.875 (26.372) | 0.176 (0.102)+ | 13.325 (3.070)*** |
| category_C | 0.373 (0.129)** | 23.146 (45.943) | 0.373 (0.129)** | 13.867 (3.512)*** |
| category_D | 0.080 (0.157) | -23.405 (42.178) | 0.080 (0.157) | 11.203 (3.268)*** |
| category_E | -0.234 (0.249) | 21.054 (99.205) | -0.235 (0.249) | -4.812 (15.672) |
| category_F | 0.304 (0.273) | 54.424 (207.594) | 0.304 (0.273) | 18.488 (6.250)** |
| category_G | 0.209 (0.297) | -1.213 (387.004) | 0.209 (0.297) | 3.519 (12.635) |
| category_H | -0.441 (0.339) | 33.324 (83.521) | -0.442 (0.339) | 24.541 (13.078)+ |
| category_I | -0.093 (0.463) | -23.836 (57.554) | ||
| category_J | -0.838 (0.572) | 295.892 (1067.204) | -0.838 (0.572) | 2.172 (13.211) |
| category_K | 0.754 (0.572) | 141.996 (2253.822) | 0.754 (0.572) | 25.843 (28.726) |
| category_L | 0.737 (0.825) | 95.316 (665.690) | ||
| category_M | -0.134 (1.246) | 120.602 (1057.772) | ||
| category_N | -2.540 (1.290)* | -3556.531 (8122.758) | ||
| category_O | -3.439 (1.637)* | -810.824 (10274.879) | ||
| category_P | 0.312 (1.953) | 166.373 (392.395) | ||
| category_Q | 0.894 (1.953) | -351.158 (1254.823) | ||
| category_R | 5.194 (31.086) | -511.573 (14024.161) | ||
| category_S | -5.106 (51.303) | -5107.558 (34637.832) | ||
| Num.Obs. | 300000 | 300000 | 299883 | 299883 |
| R2 | 0.145 | 0.145 | ||
| R2 Adj. | 0.144 | 0.144 |
表1-2:被説明変数が金額の合計(Receiverの属性)
|
OLS
|
IV
|
OLS2
|
IV2
| |
|---|---|---|---|---|
| r_sexf | 0.936 (0.014)*** | 1.018 (0.181)*** | 0.936 (0.014)*** | 0.951 (0.022)*** |
| r_age15-19 | 0.259 (0.048)*** | 0.308 (0.442) | 0.258 (0.048)*** | 0.240 (0.051)*** |
| r_age20-24 | 1.296 (0.055)*** | 1.402 (0.444)** | 1.296 (0.055)*** | 1.273 (0.058)*** |
| r_age25-29 | 1.601 (0.064)*** | 1.799 (0.588)** | 1.601 (0.064)*** | 1.590 (0.067)*** |
| r_age30-34 | 1.351 (0.069)*** | 1.599 (0.718)* | 1.349 (0.069)*** | 1.347 (0.073)*** |
| r_age35-39 | 0.799 (0.070)*** | 1.084 (0.856) | 0.798 (0.070)*** | 0.783 (0.075)*** |
| r_age40-44 | 0.408 (0.072)*** | 0.472 (0.477) | 0.407 (0.072)*** | 0.375 (0.076)*** |
| r_age45-49 | 0.208 (0.072)** | 0.260 (0.817) | 0.207 (0.072)** | 0.167 (0.078)* |
| r_age50- | -0.407 (0.069)*** | -0.174 (0.773) | -0.407 (0.069)*** | -0.440 (0.083)*** |
| r_occupation1 | 0.927 (0.031)*** | 0.922 (0.150)*** | 0.927 (0.031)*** | 0.931 (0.032)*** |
| r_occupation2 | 1.522 (0.040)*** | 1.493 (0.339)*** | 1.523 (0.040)*** | 1.535 (0.041)*** |
| r_occupation3 | 1.521 (0.047)*** | 1.514 (0.322)*** | 1.522 (0.047)*** | 1.523 (0.050)*** |
| r_occupation4 | 2.174 (0.467)*** | 1.155 (2.545) | 2.176 (0.467)*** | 1.910 (0.484)*** |
| r_occupation5 | 1.571 (0.051)*** | 1.430 (0.725)* | 1.573 (0.051)*** | 1.580 (0.054)*** |
| r_occupation6 | 1.240 (0.062)*** | 0.964 (1.095) | 1.240 (0.062)*** | 1.237 (0.066)*** |
| r_occupation7 | 1.073 (0.084)*** | 0.813 (0.571) | 1.075 (0.085)*** | 1.067 (0.093)*** |
| r_occupation8 | 1.287 (0.070)*** | 1.156 (1.940) | 1.287 (0.070)*** | 1.279 (0.075)*** |
| r_occupation9 | 1.543 (0.061)*** | 1.189 (1.605) | 1.545 (0.061)*** | 1.612 (0.066)*** |
| r_occupation10 | 1.197 (0.104)*** | 0.888 (0.434)* | 1.200 (0.104)*** | 1.163 (0.114)*** |
| l_r_friend | 0.517 (0.009)*** | 0.592 (0.199)** | 0.517 (0.009)*** | 0.519 (0.010)*** |
| Num.Obs. | 300000 | 300000 | 299883 | 299883 |
| R2 | 0.145 | 0.145 | ||
| R2 Adj. | 0.144 | 0.144 |
表1-3:被説明変数が金額の合計(その他重要そうなもの)
|
OLS
|
IV
|
OLS2
|
IV2
| |
|---|---|---|---|---|
| is_coupon | 1.022 (0.024)*** | 1.188 (0.304)*** | 1.022 (0.024)*** | 0.994 (0.025)*** |
| is_egift | -0.424 (0.100)*** | 11.228 (23.037) | -0.424 (0.100)*** | 10.990 (2.841)*** |
| is_birthday | 0.299 (0.031)*** | 0.126 (1.768) | 0.299 (0.031)*** | 0.285 (0.038)*** |
| is_open | 0.160 (0.020)*** | 0.043 (1.525) | 0.160 (0.020)*** | 0.148 (0.023)*** |
| l_selling_price | 0.175 (0.007)*** | 0.285 (0.139)* | 0.174 (0.007)*** | 0.184 (0.011)*** |
| l_order_14 | 0.104 (0.006)*** | 0.009 (0.126) | 0.104 (0.006)*** | 0.100 (0.011)*** |
| l_pv_14 | -0.016 (0.003)*** | -0.019 (0.073) | -0.016 (0.003)*** | -0.015 (0.004)*** |
| l_day_selling | 0.032 (0.015)* | -0.072 (0.412) | 0.032 (0.015)* | 0.021 (0.019) |
| is_birthday × is_open | -0.173 (0.034)*** | -0.166 (1.731) | -0.172 (0.034)*** | -0.173 (0.038)*** |
| Num.Obs. | 300000 | 300000 | 299883 | 299883 |
| R2 | 0.145 | 0.145 | ||
| R2 Adj. | 0.144 | 0.144 |
表2:被説明変数(商品カテゴリ)
|
logit
|
logit2
|
OLS2_p
|
IV2_p
|
AME(logit)
|
AME(logit2)
| |
|---|---|---|---|---|---|---|
| category_B | 0.045 (0.059) | 0.044 (0.059) | 0.009 (0.013) | 1.355 (0.380)*** | 0.010 | 0.010 |
| category_C | 0.118 (0.074) | 0.118 (0.074) | 0.026 (0.016) | 1.387 (0.428)** | 0.026 | 0.026 |
| category_D | -0.025 (0.088) | -0.025 (0.088) | -0.007 (0.020) | 1.015 (0.406)* | -0.005 | -0.005 |
| category_E | -0.177 (0.142) | -0.177 (0.142) | -0.041 (0.031) | -0.423 (2.062) | -0.038 | -0.038 |
| category_F | 0.128 (0.150) | 0.128 (0.150) | 0.029 (0.034) | 1.967 (0.781)* | 0.028 | 0.028 |
| category_G | 0.064 (0.170) | 0.064 (0.170) | 0.012 (0.038) | 0.352 (1.516) | 0.014 | 0.014 |
| category_H | -0.349 (0.195)+ | -0.349 (0.195)+ | -0.075 (0.041)+ | 3.023 (1.794)+ | -0.076 | -0.076 |
| category_I | 0.043 (0.275) | 0.009 | ||||
| category_J | -0.500 (0.317) | -0.500 (0.317) | -0.114 (0.074) | -0.120 (1.668) | -0.109 | -0.109 |
| category_K | 0.347 (0.326) | 0.347 (0.326) | 0.076 (0.072) | 4.006 (3.655) | 0.075 | 0.075 |
| category_L | 0.421 (0.453) | 0.091 | ||||
| category_M | -0.128 (0.615) | -0.028 | ||||
| category_N | -1.653 (0.842)* | -0.359 | ||||
| category_O | -2.015 (1.133)+ | -0.437 | ||||
| category_P | 0.303 (1.102) | 0.066 | ||||
| category_Q | 0.672 (0.937) | 0.146 | ||||
| category_R | 7.286 (1.004)*** | 1.581 | ||||
| category_S | -8.303 (1.003)*** | -1.802 | ||||
| Num.Obs. | 300000 | 299883 | 299883 | 299883 | ||
| R2 | 0.131 | |||||
| R2 Adj. | 0.131 |
※表の上の星はp値を表しています(+=.1, *=.05, **=.01, ***=0.001)。
※AME = Average Marginal Effect、ロジットモデルにおける確率への(平均的な)限界的な効果として解釈できる。
説明・考察
表1は被説明変数が金額の合計になっている場合について、表2は被説明変数がギフトを使用するかしないかのダミー変数に�なっているケースについて表しています。
被説明変数:金額の合計
表1について、まずすべての説明変数を用いて回帰を行なったのがOLS、 IV、logitです。これらをみる限り、表1−2が表しているようにReceiverの属性はその後の購入金額や購入をするか否かに影響を与えているのに対して、表1ー1が表している通り、商品のカテゴリはCを除くと、概ね大きな影響を与えていないことが分かります(強いて言えばNとOの係数は有意です。ただ、そもそも全体に占める数が少ないというのもあり、重要かと言われるとそうではないと考えられます)。
ここで、IV推定量についてWeak instrument problemを考えます。IV推定量においては、内生変数と操作変数の相関があまりにも弱いと、正しい推定が行われなくなってしまうことが知られています。本来、内生変数が複数あるケースの場合はCragg-Donald Wald F statisticを用いるのが良いとされていますが、計算量の問題で実現しなかったため、一段階目の推定(IV推定は点推定の意味では二段階のOLSと一致します。そして、特に内生変数が一つだけの時には一段階目の推定によってweak instrumentが判断されます)でweak instrument problemが明らかに疑われるカテゴリについて、データごと落としたものがOLS2、 IV2です。
まず、OLSとOLS2については推計結果にあまり差が見られないため、(厳密ではないですが)上記で落とした変数の影響はさほどないように見えます。そして、IV2を見る限り、特にB, C, D, Fが非説明変数に大きな影響を与えているであろうことがわかります。よって、Receiverが何を貰う傾向にあるかというのをコントロールした場合、B, C, D, Fはその後のReceiverの購入金額を増加させるのではないかということが見て取れます。解釈としては難しいところですが、例えば普段からB関連のものを使っている人だけではなくて、一般にB関連の物を渡された場合に、その後LINEギフトを使用しようという気持ちが大きくなるのではないかということができます。
また補足として、IV2においてHausman検定ではOLSとIVの結果が同じであるという帰無仮説が棄却され、Over-identification検定では操作変数と誤差項が無相関であるという帰無仮説を棄却できませんでした。よって今回の操作変数を用いたモデルは妥当性があると判断します。
被説明変数:ダミー変数
次に表2について、logitはOLSやIVと同じように全ての変数を用いてロジスティック回帰をしたものです。全体的にOLSと同様の傾向が見られます。ただし、OLSと同じく内生性の問題が疑われます。
そこで、OLS2やIV2と同じデータや変数を用いたのがlogit2、OLS2_p、IV2_pです。OLS2_p、IV2_pは線形確率モデルを用いていることになります。おおまかな係数の有意性や正負は被説明変数が購入金額の合計であったケースと一致していることがわかります。
※上記では基本的に有意水準を5%としています
展望・やるべきこと
今回はここまでで分析が終わってしまいましたが、今後やるべきこととして挙げられるのが、今回特に効果が高いという結果になった係数について、実際にReceiverがその後どのような購入を見せているかと言う点を個別に見ていくと言う点でしょう。それを見ていくことで、今回の結果を検証できるとともに、どういった要因でReceiverのその後の購入が行われているかについて、より解像度高く理解することが可能となるでしょう。
また、Senderのクーポン使用はコントロールしているものの、Receiverのクーポン使用に関して、(Senderのクーポン使用や月ダミーである程度コントロールできるかもしれないものの)クーポンの効果を完全にコントロールできていない懸念があります。Receiverがクーポンを使用しているかといったダミー変数や各説明変数との交差項を変数に入れる必要があるかもしれません(ただし交差項を入れた場合、操作変数を使うことが難しくなる)。なお、今回はご紹介していませんが、モデルの検証のために観察期間をずらして推定を行いました。結果はあまり変わらなかったため、モデルの係数の推定値はロバストで、Receiverのクーポン使用可否による影響はあまりないと言えるかもしれません。
加えて、今回二項モデルについて操作変数を用いた分析を深掘りできていない点も心残りです。またそもそもモデルに関する点でいうと、そもそも購入金額は0未満を取ることのできない変数であるために、それを考慮したモデルを使用するべきかもしれません。
最後に、仮に同じような趣味を持つ人同士でLINEギフトを贈り合うことを考えると、操作変数の妥当性が疑われ�ます。そのため、より良い操作変数をみつけることも必要かもしれません。
感想
今回、6週間にわたってインターンに参加させていただき、LINE株式会社の皆様、とりわけDSチームやその中でもギフトに関わる皆様には大変お世話になりました。特にメンターの橋本さんや上長であった岡田さんには様々なアドバイスをいただくことができました。経済学バックグラウンドの方やそうではないデータサイエンティストの方の双方の視点が得られたのはとても学びになりましたし、ありがたかったです。
フルタイムでDSのチームに参加させていただくという貴重な機会であり、実際の事業で得られた広大なデータを分析するという経験を得られたとともに、その面白さや大変さ、どのように価値のある分析をすればいいのかという点の難しさを学ぶことができ、とても有意義な時間であったと思っています。また実際のビジネスの分析で行われる、着手する前に分析設計をしてそれを他の方にレビューしていただくというフローを経験できたのは貴重な体験でしたし、効率的な分析をする上での学びがありました。
惜しむらくは、最終的に仕上げる分析のテーマがなかなか決まらずに、本分析に2週間弱しかかけられず、多少中途半端な状態に終わってしまったことです。DSチームの方に最初にご挨拶した際に、6週間は長いようで意外と短いよと言われていたのですが、それを身を持って実感しました。総じて大変良い経験をさせていただいたと思っています。
付録
最後に上記で用いた用語について簡単に解説をします。以下の説明��は厳密性を失っている(ないし誤りを含む)恐れがあるため、正確な理解をしたい場合は教科書等を読んでください、、
OLSってなあに
端的に言えば説明変数と被説明変数の線形な関係を表したいときに用いられる方法です。次のようなモデルを考えます。
※ここ
ただし、iは各サンプルを、kは説明変数の数を、Yiは各サンプルの被説明変数を、Xijはサンプルiのj番目の説明変数を、eiはiの誤差項を表しています。ここで、サンプルサイズをnとして とすると、以下のような行列の形で書くこともできます。
このとき、OLS推定量は以下の最小化問題を解いて得られます。
これを解くと、OLS推定量は以下の形で書くことができます。
行列の形で書くと以下のようになります。
IVってなあに
OLSはある一定の仮定のもとで一致性(Consistency, i.e. converges in probability to )を持ちます。そのうちの一つが、です。これは、端的にいうと説明変数と誤差項が無相関であることを意味します。しかしながら、往々にしてこの仮定が満たされないことがあります。
今回のケースでは、私は誤差項にReceiverの趣味が入っている可能性を考えました。SenderがReceiverに何を贈るかはReceiverの趣味が影響を与えるでしょう。そして、Receiverの趣味がReceiverがその後ギフトを使うのかに影響を与えるとすれば、内生性(endogeneity)の問題が発生していることになります。
その対象方法として操作変数法というものが知られています。これはを満たすような操作変数(instrumental variable)Zを用いるというものです。
今回のケースでは操作変数としてSenderが普段どのようなカテゴリのものを贈っているかを用いました。これは、Receiverの趣味とは相関しないけれど、Senderが何を贈るかには相関するであろうと考えられるためです。(ただし、同じような趣味を持つ人同士でLINEギフトを贈り合うことが一般的であると考えられるのであれば、この仮定は崩れてしまうことになります、、)
以下では内生変数と操作変数の次元の数が等しい場合、すなわち丁度識別(just identified)を考えます。IV推定量はモーメント推定量の一種です。すなわち、我々は
というモーメント条件を得ています。そして、これは
に等しいです。よって、我々はβの推定量を
を解くことによって得ることができます。IV推定量は以下のように書くことができます。
行列の形だと、以下のようになります。
そして、操作変数の次元が内生変数の次元を上回っている場合、過剰識別(over identified)と呼ばれ、上記の方法では計算ができません。よって、下記の2SLS推定量が用いられます。
ただし、です。
これらのIV推定量は二段階のOLSと一致することが知られています(2SLS, two-stage least squares)。すなわち、XをZに回帰させてXの予測値を得て、そのでYを回帰するというものです。これは、ZでXを説明できる部分だけでYを説明していると解釈することができます。
logitってなあに
特に経済学の世界では、ものを買うか買わないかの様な離散選択を扱う際にロジスティック回帰というかっこいい名前の回帰を用います。
なぜ上記のようなOLSではないのでしょうか? 正直なところ別にダメというわけではありません。OLSを2項選択を扱う際に用いるのであれば、とすることができます。しかしながら、この場合だと例えばその商品を買う確率が1を超えるというような些かおかしなことが起きてしまうのです。
そのため、ロジットモデルのような非線形のモデルを用います。F(・)を適当な連続確率変数の分布関数とするとき、非線形モデルは
とすることができます。このときに、ロジスティック分布の分布関数を用いればロジスティック回帰になります。
このとき、最尤法を用いて推定することになります。Yの条件付き確率関数は
となるので、以下の対数尤度関数を最大化することで推定量を得ることができます。
Heteroskedasticity-robust standard error(不均一分散に対して頑健な標準誤差)
回帰分析をする際には、伝統的にが一定であるという仮定が置かれます。これをHomoskedasticityと呼びます。そして、その仮定のもと標準誤差(standard error)が計算されます。しかしながら、特に経済学の世界ではこの仮定は一般的に成り立つとは考えられていません。よって、その仮定を前提としないHeteroskedasticity-robust standard errorが用いられるべきであるとされています。これにはいくつか種類があり、HC0, HC1, HC2, HC3, HC4が提案されているようです。
参考文献
末石 直也(2015)『計量経済学 -ミクロデータ分析へのいざない』日本評論社.
Hansen, B. E. (2022). Econometrics. Princeton University Press.