Jira의 이슈 정렬 방식이 Integer 방식이 아니라고?!

들어가며

안녕하세요. LINE+ Contents Service Engineering 조직에서 백엔드 개발을 하고 있는 김한솔, 문다정, 이현동, 조강훈입니다. 저희 조직에서는 그룹 구성원의 기술 성장을 돕고 향상된 능력을 적재적소에 활용할 수 있도록 Tech Group이라는 조직 내 스터디 그룹을 운영하고 있습니다. 이 글에서는 Tech Group을 운영하면서 다뤘던 여러 주제 중 하나인 Atlassian Jira의 랭킹 알고리즘, LexoRank를 소개하려고 합니다.

LexoRank는 드래그 앤드 드롭(drag and drop) 정렬을 효과적으로 다룰 수 있는 정렬 알고리즘입니다. Atlassian에서 기존에 사용되던 다양한 드래그 앤드 드롭 정렬 방식의 단점을 보완해 개발했는데요. Atlassian에서는 Jira에서 LexoRank 알고리즘을 사용하는 방법과 기본적인 운영 메커니즘에 관한 정보만 제공할 뿐 별도로 라이브러리를 공개하지는 않았습니다.

이 때문에 많은 사용자가 다양한 LexoRank 라이브러리를 개발해 공개했는데요. 대부분의 라이브러리가 운영 중인 서비스에 바로 적용하기에는 제약 사항이 많았습니다. 이에 저희는 다양한 서비스에 효과적으로 적용할 수 있는 LexoRank 라이브러리를 직접 개발했고, 이를 사내 임직원을 위한 사내용 오픈소스로 공개했습니다.

본 글에서는 LexoRank가 무엇인지, 다른 랭킹 알고리즘과 비교해 어떤 장점이 있는지 설명하고, LexoRank 라이브러리를 개발하면서 마주한 여러 이슈와 그 해결 과정을 공유하고자 합니다. 이 글이 여러분께 유용한 인사이트를 제공하기를 바라며, 그럼 LexoRank로 딥다이브해 보겠습니다!

드래그 앤드 드롭 구현에 사용하는 기존 랭킹 알고리즘의 종류와 한계

먼저 일반적으로 드래그 앤드 드롭 정렬을 구현하기 위해 사용하는 아래 세 가지 알고리즘이 어떻게 작동하는지 알아보고 각각 어떤 한계가 있는지 살펴보겠습니다.

Integer 방식
GreenHopper 방식
Linked List 방식

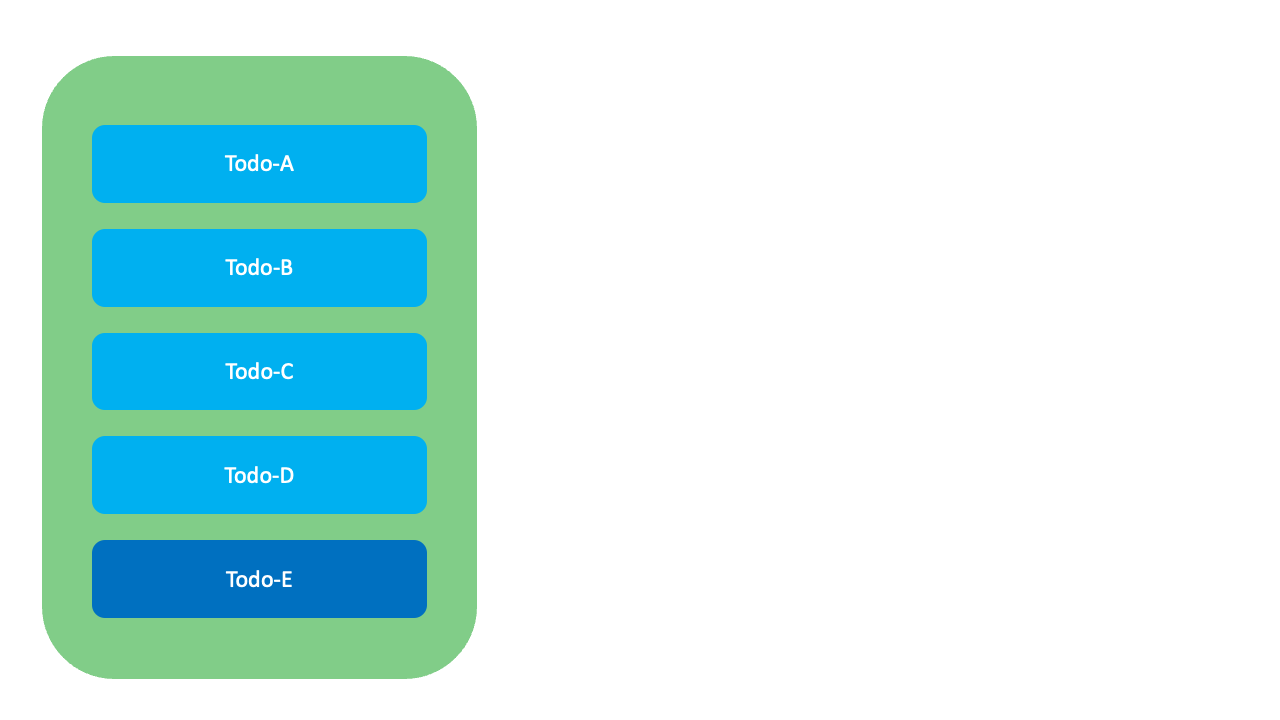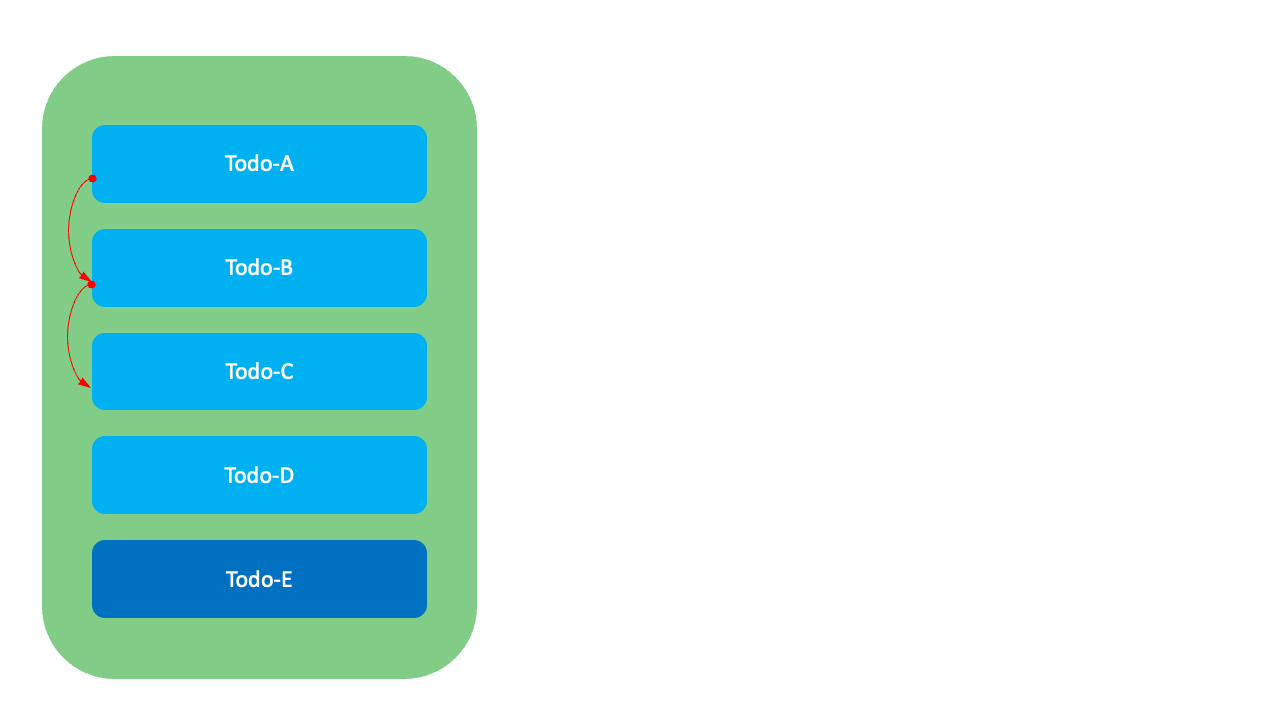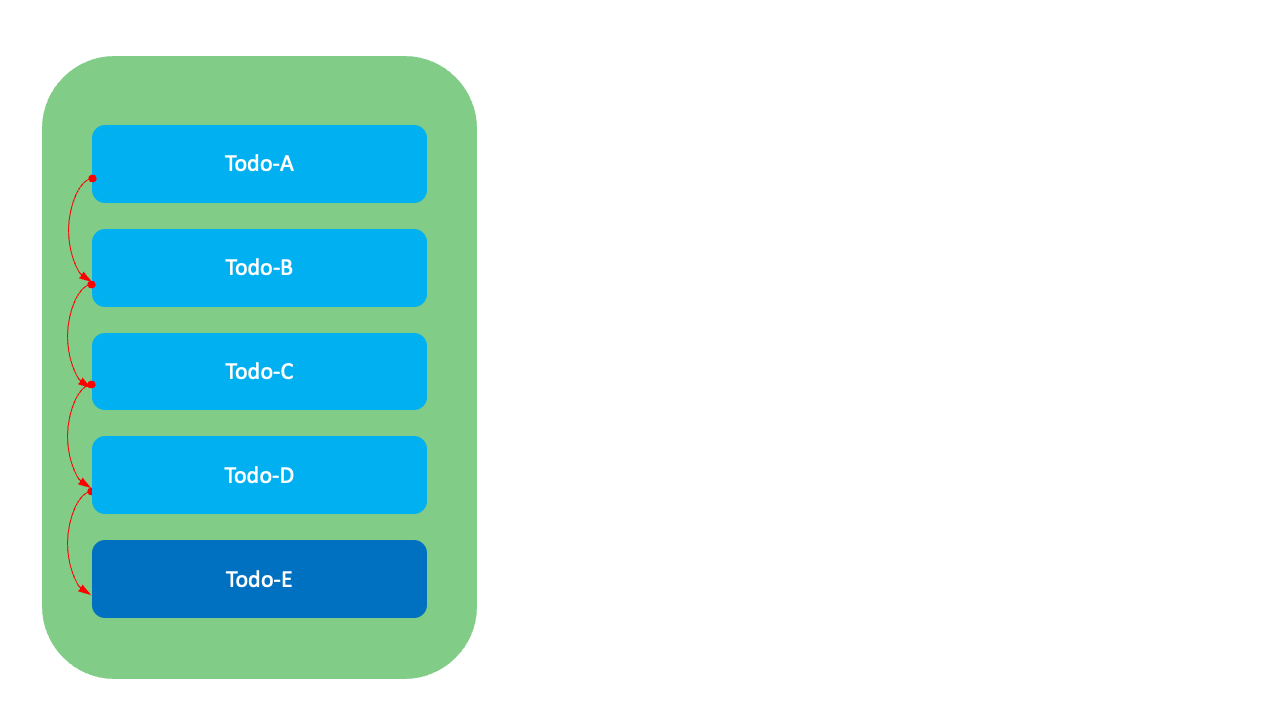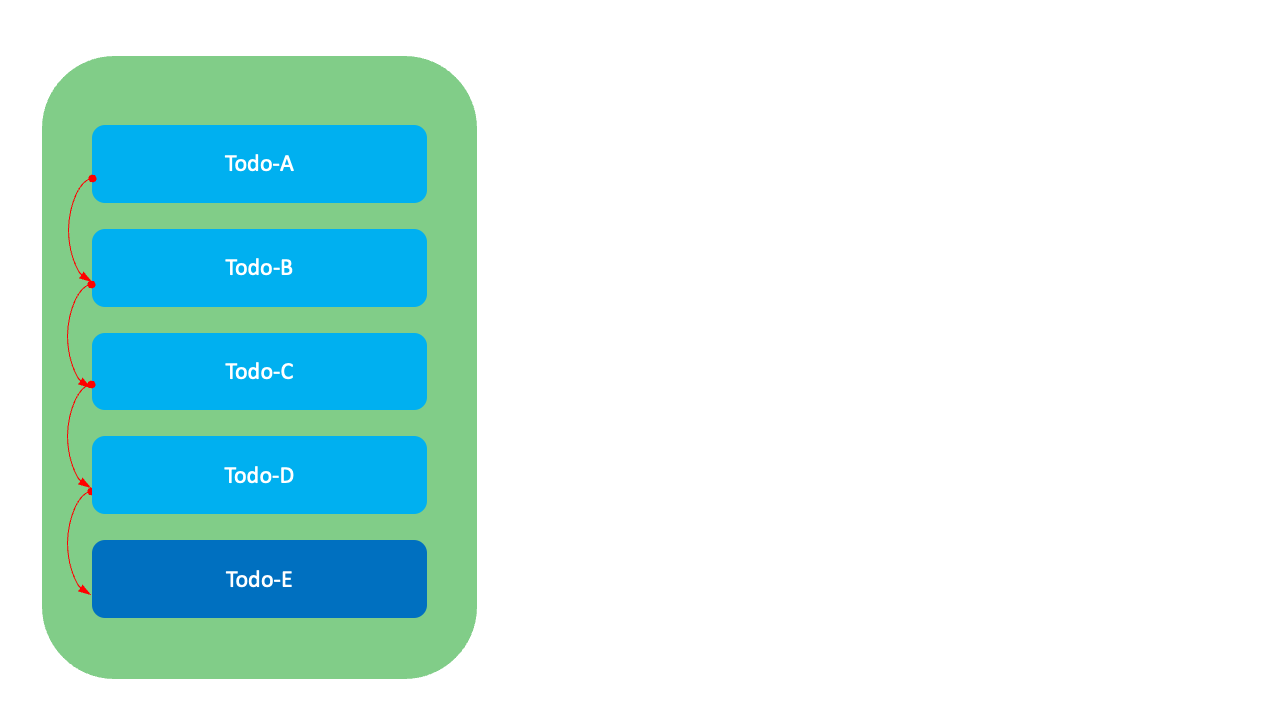
이해를 돕기 위해 할 일 목록(to-do list)에서 항목을 드래그 앤드 드롭으로 정렬하는 예시를 준비했습니다.

1. Integer 방식

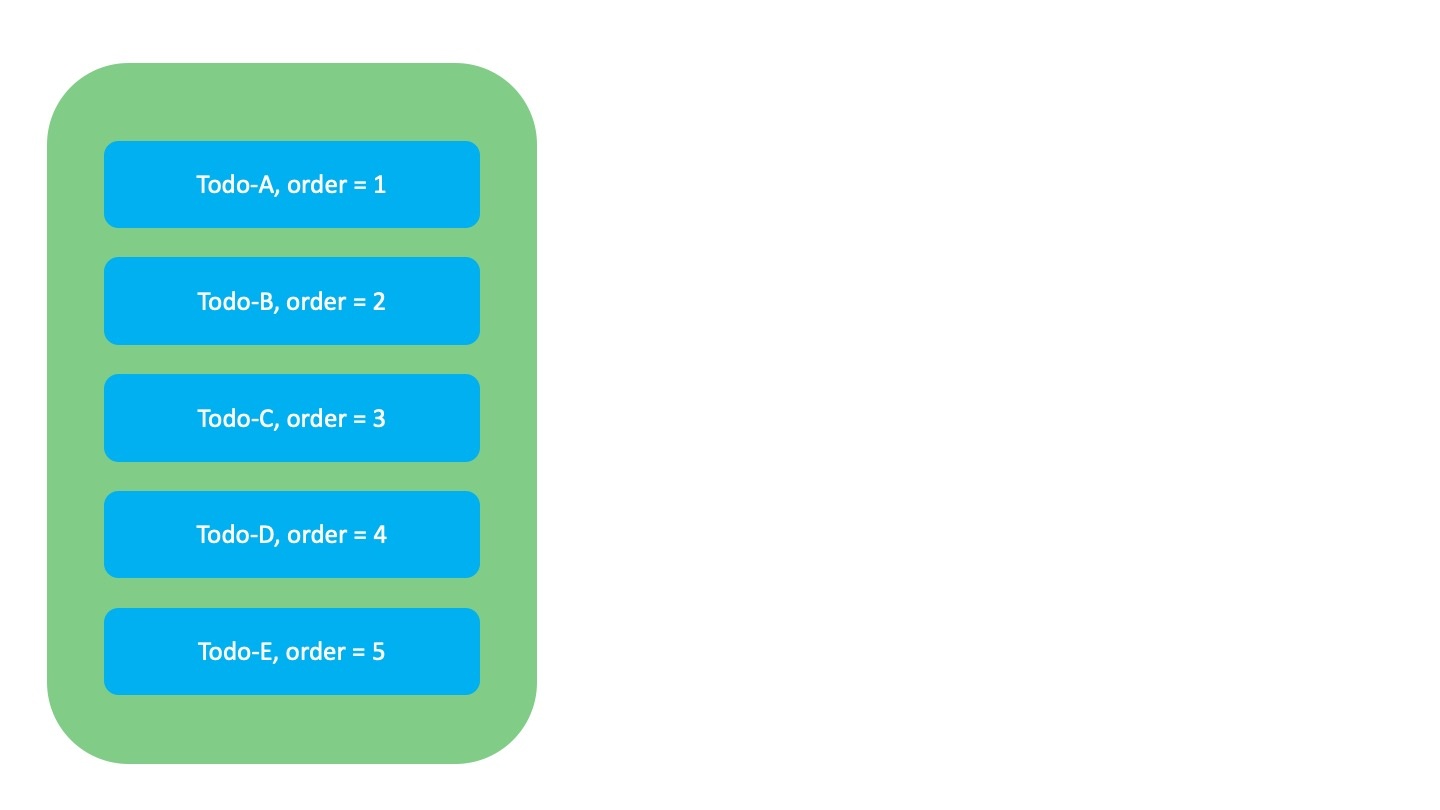
첫 번째로 가장 고전적인 방식인 Integer 방식입니다. 이 방식은 아래 그림과 같이 각 항목의 순서를 연속된 정수로 저장하는 방법입니다.

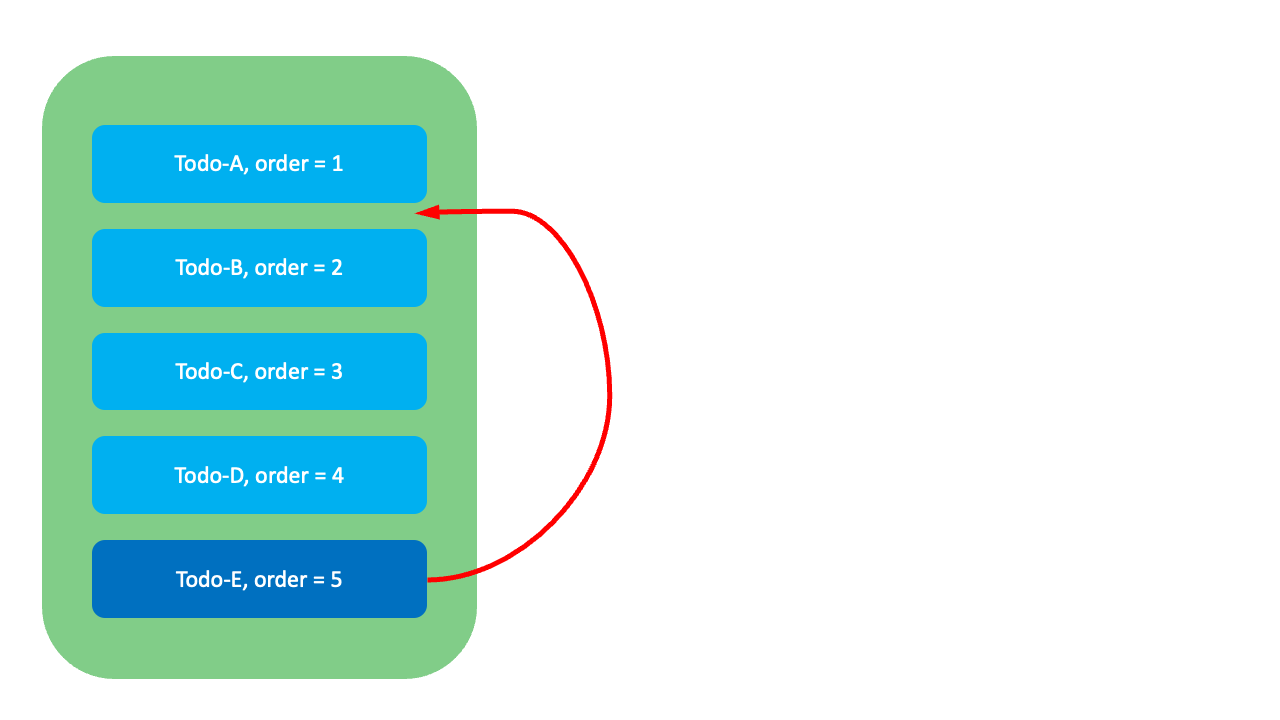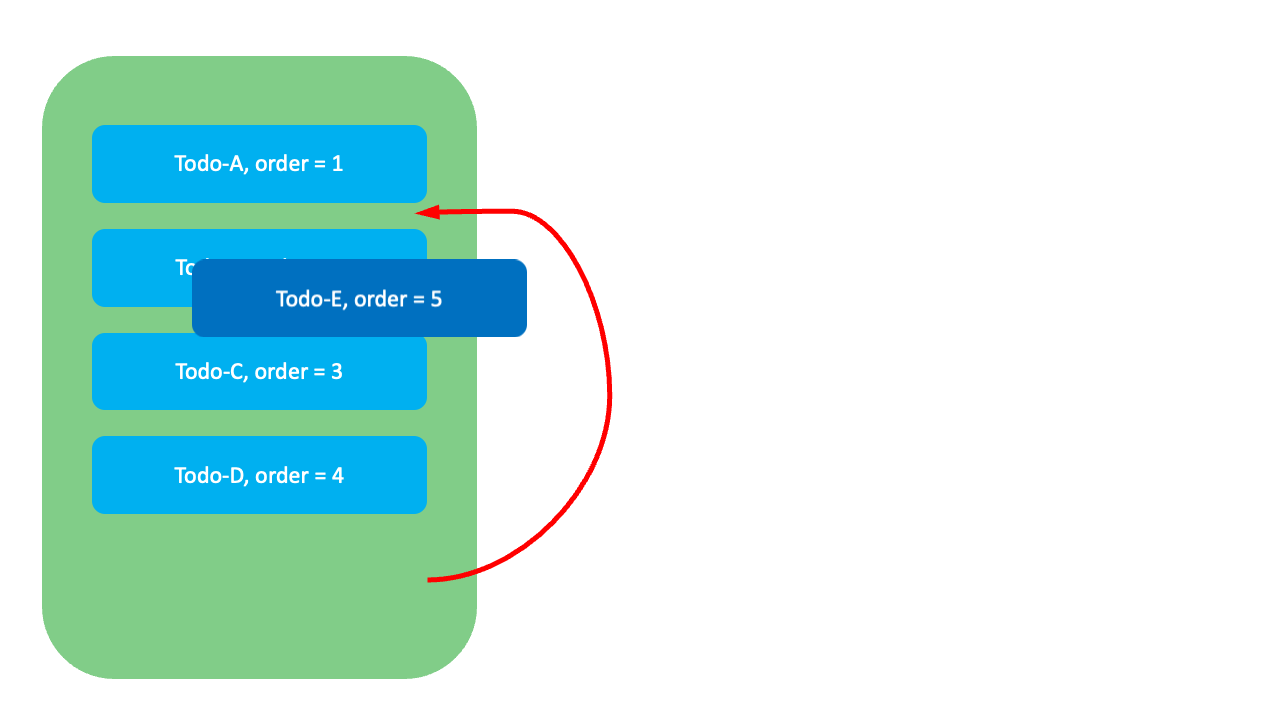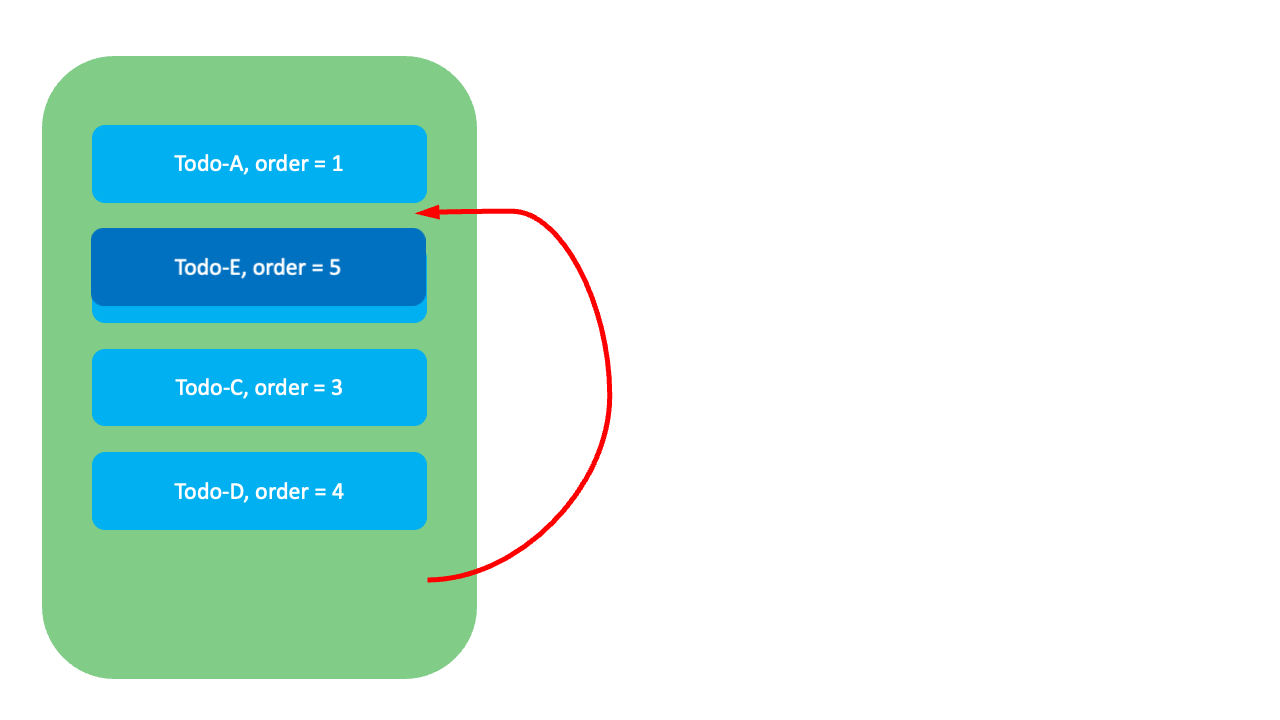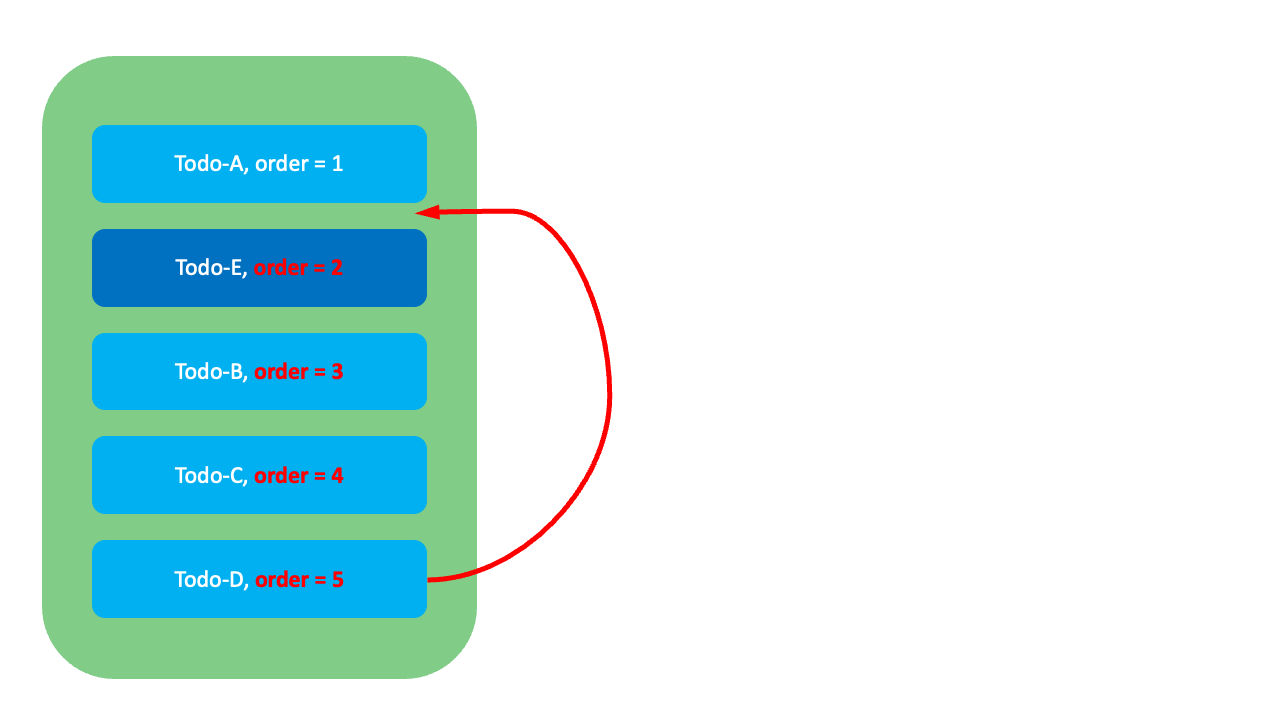
이 방식에는 어떤 한계가 있을까요? 예를 들어, 아래 그림과 같이 맨 아래에 위치한 Todo-E의 순서를 Todo-A와 Todo-B 사이로 변경하고 싶다고 가정해 봅시다. 이 경우 Todo-E의 순위값(order)이 5에서 2로 변경되며, 이후 기존 순서를 유지하기 위해 하위 항목들인 Todo-B, Todo-C, Todo-D의 순위값을 수정해야 하고, 수정하는 동안 시스템은 중단됩니다. 이런 방식은 데이터가 많은 경우 시스템의 성능 저하를 일으킬 수 있으며, 동시에 여러 사용자가 수정을 시도하면 빈번하게 충돌이 발생하기도 합니다.

2. GreenHopper 방식

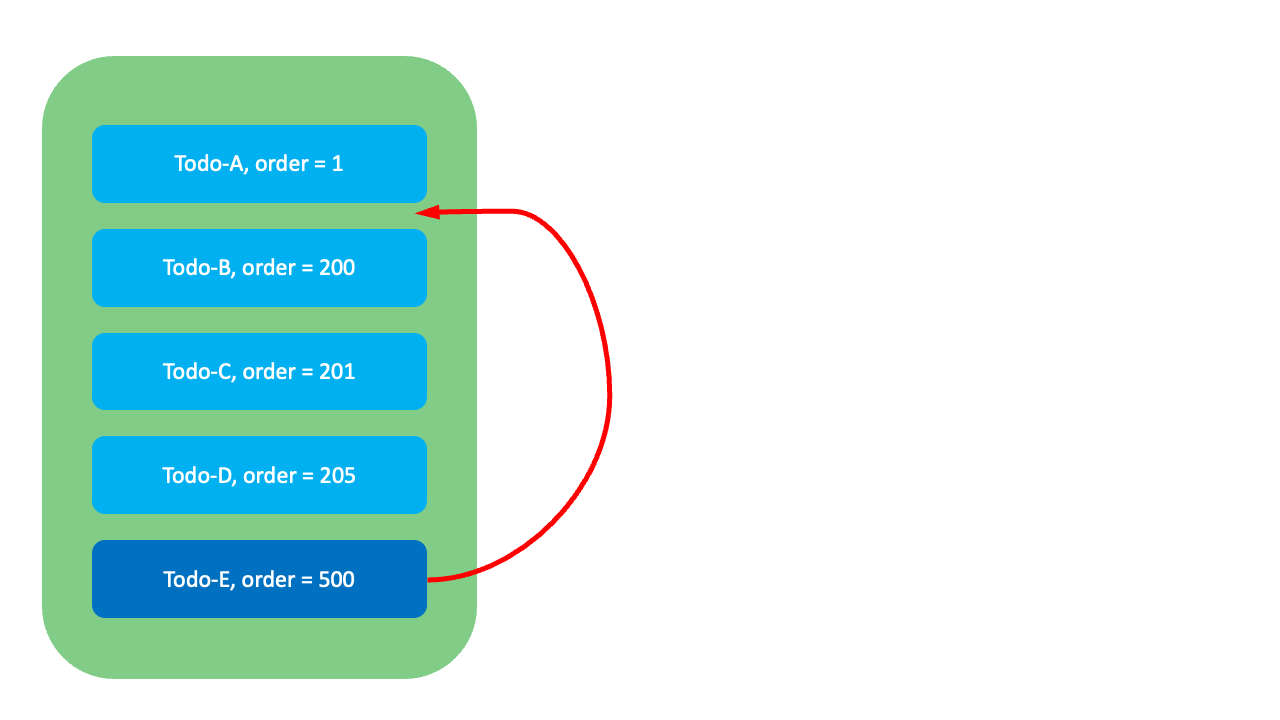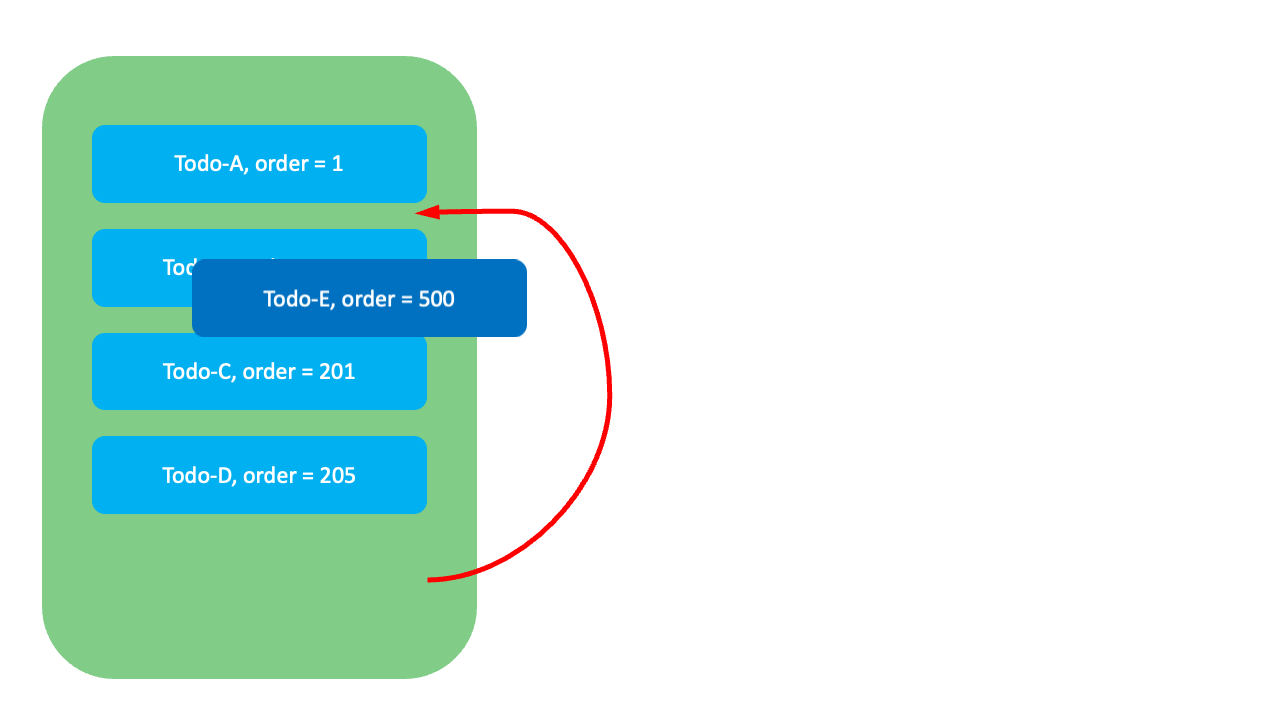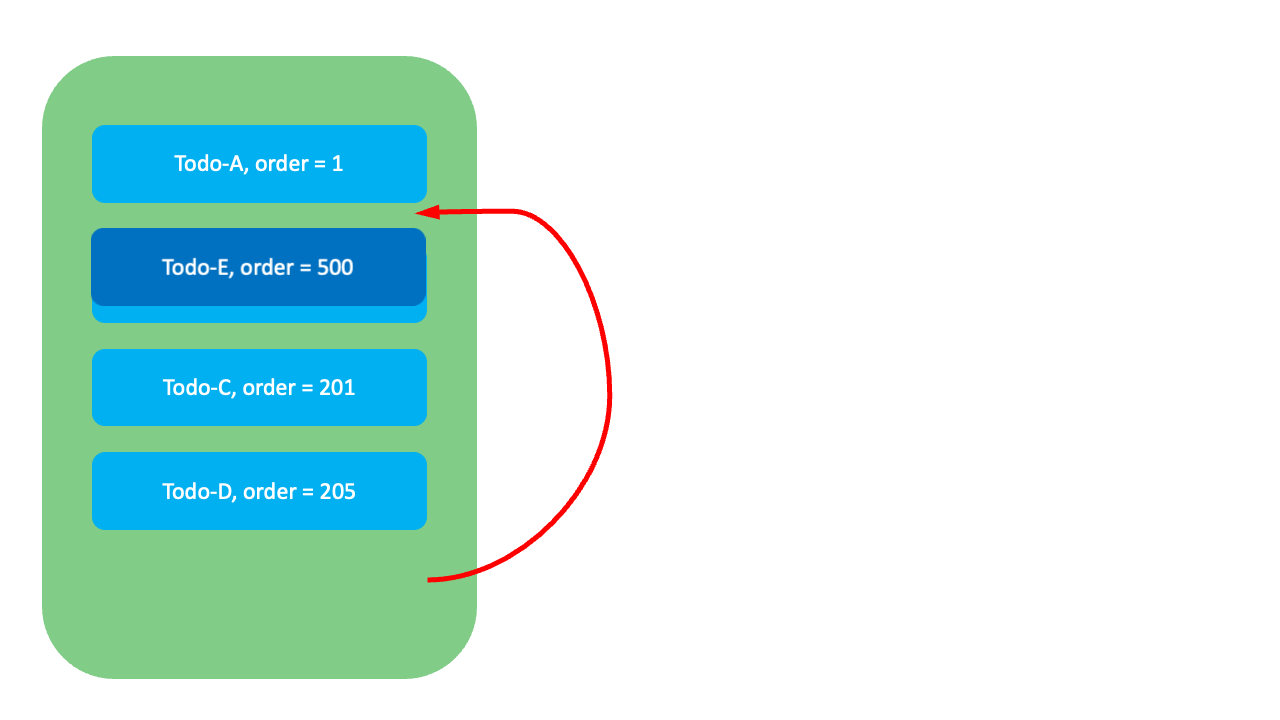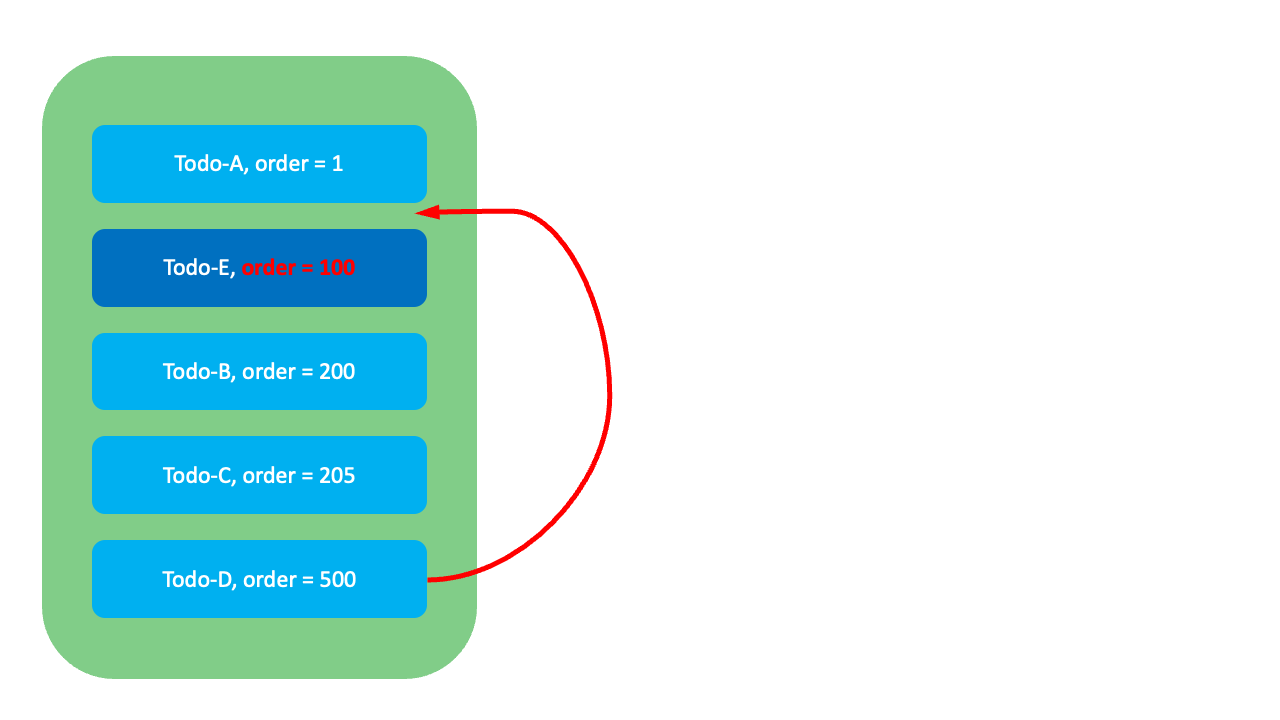
이 방식은 정수 방식과 유사하지만, 각 항목 사이에 충분한 간격을 두고 순위값을 할당해서 새 항목을 중간에 삽입할 때 Todo-E외에 다른 항목의 순위값은 변경하지 않아도 됩니다. 예를 들어, Todo-E를 Todo-A와 Todo-B 사이로 옮길 때 Todo-E의 순위값을 100으로 수정하기만 하면 됩니다.

GreenHopper 방식에도 한계는 있습니다. 아래와 같이 이미 순위값들이 밀집돼 있어 새로운 값을 부여할 여유가 없는 상황이라면, 시스템을 중단하고 순위값을 재조정(rebalancing)하는 작업이 필요하며, 이때 정수 방식과 동일한 한계에 부딪힙니다.

3. Linked List 방식

이 방식은 각 항목이 이전 항목과 다음 항목의 정보를 갖고 있는 방식입니다. 따라서 GreenHopper 방식에서 발생하는 순위값 고갈 현상은 발생하지 않습니다.

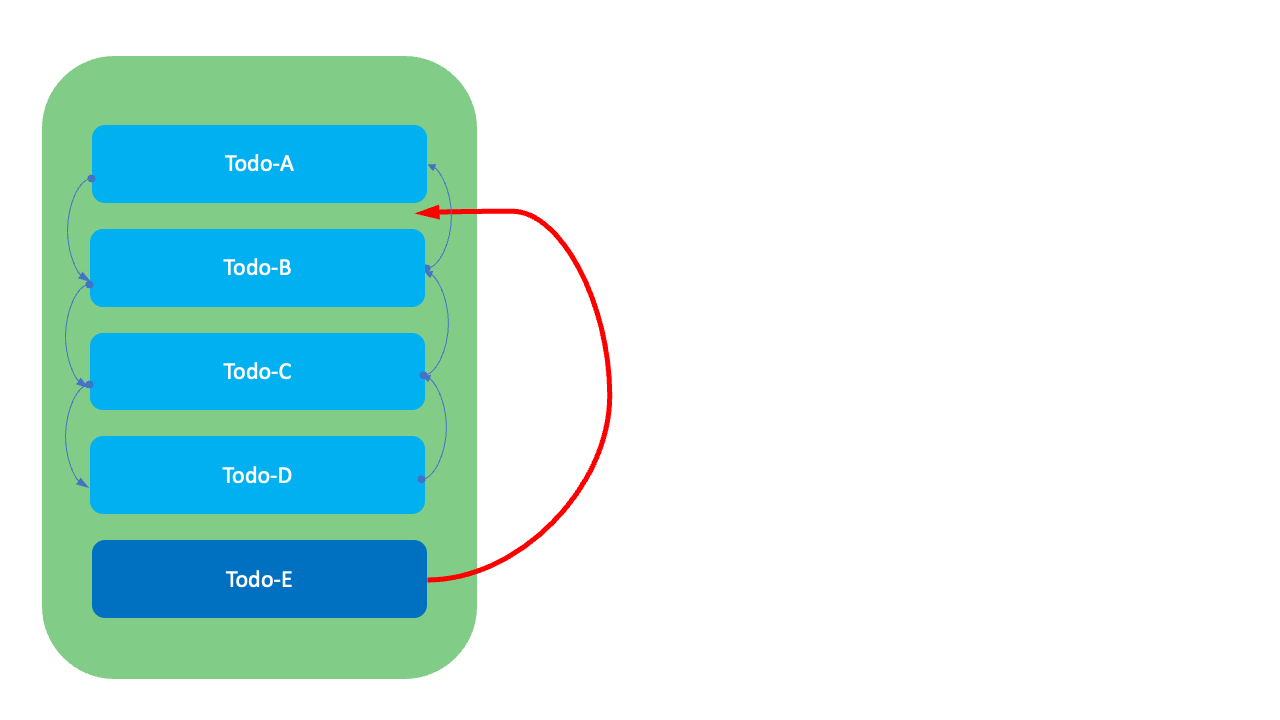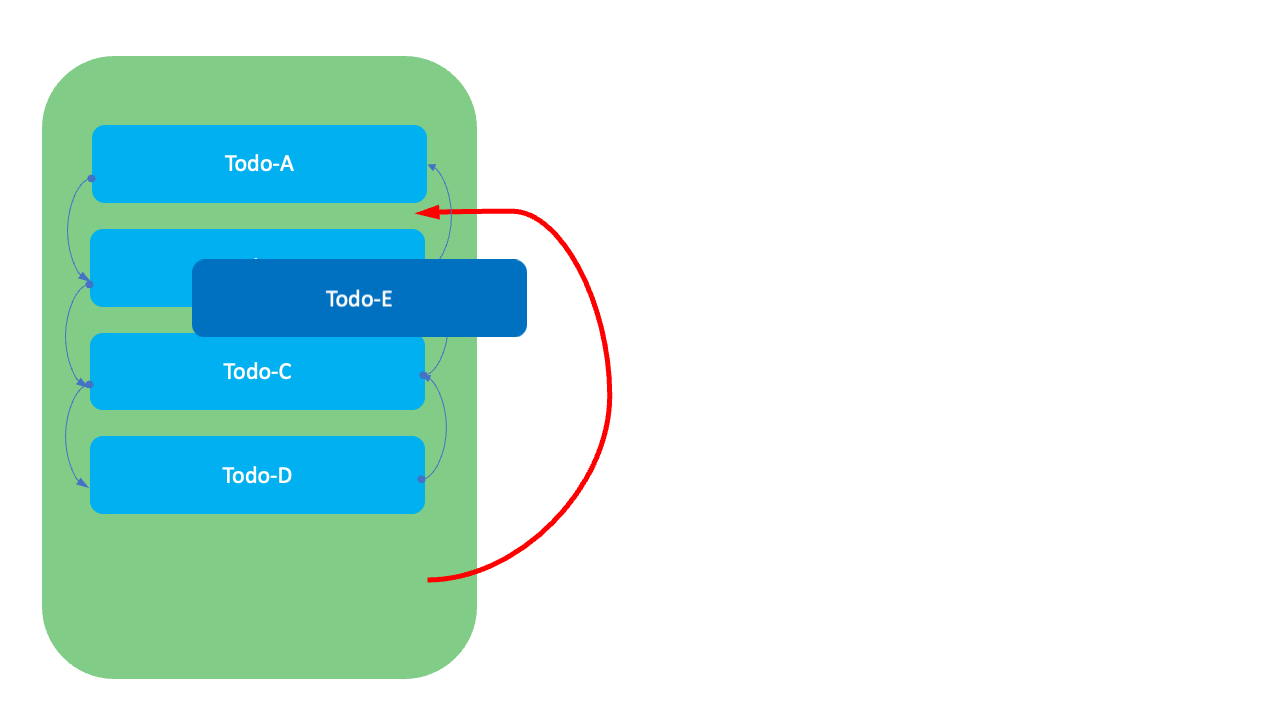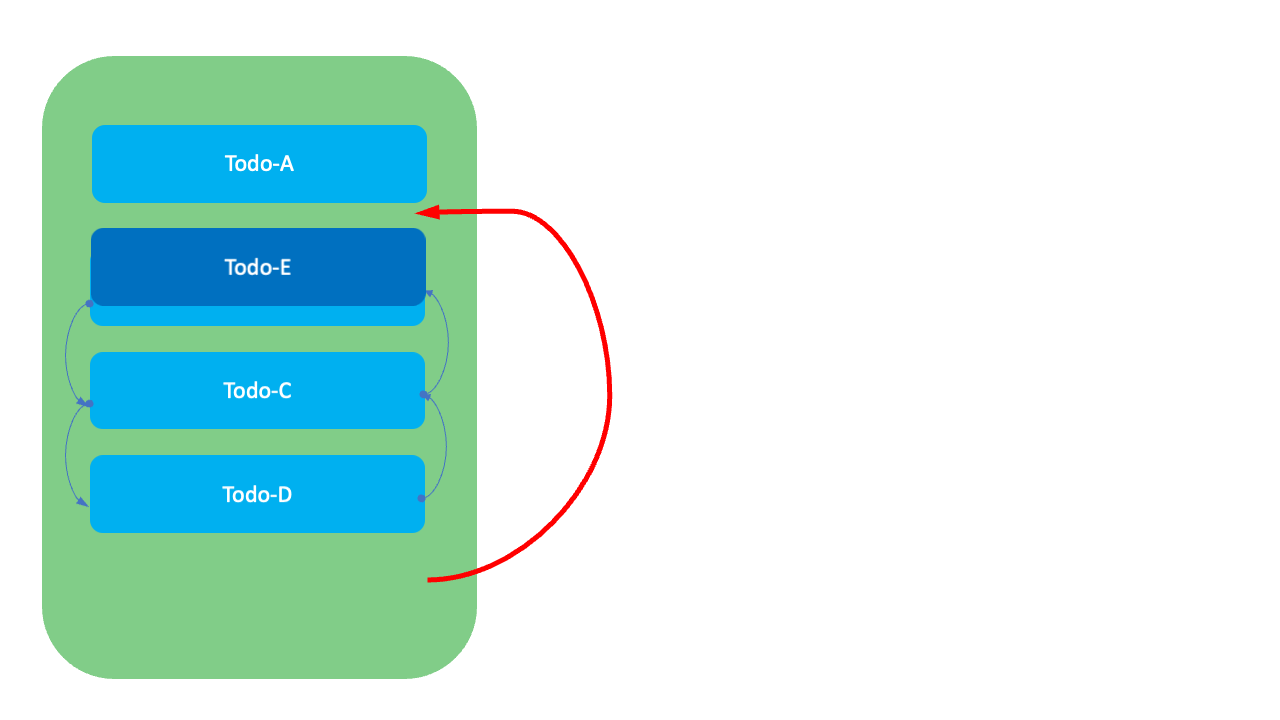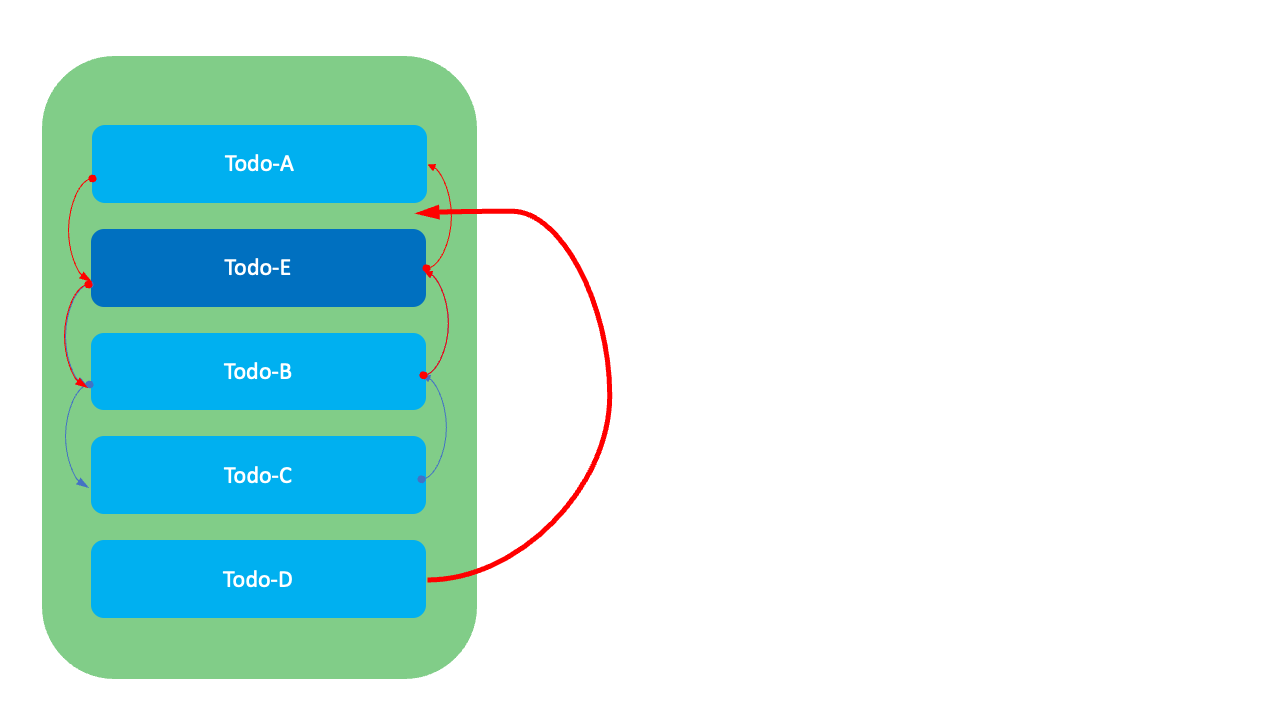
하지만 이 방식에서는 순서를 변경할 때 연결된 항목들의 이전과 다음 항목 정보를 수정하기 위한 2~4번의 수정 비용이 발생합니다. 또한 목록을 조회할 때 전체를 스캔(full scan)해야 한다는 단점이 있습니다.

이와 같이 기존 랭킹 시스템은 데이터가 많고 드래그 앤드 드롭이 빈번하게 발생하는 상황에서는 명확한 한계를 드러냅니다.

정렬 방식	주요 한계점
Integer	순서 변경 시 수정 범위가 큼(O(N))
GreenHopper	빠른 Rank 고갈 및 재조정 시 시스템 중단
Linked List	순서 변경 시 2~4번의 고정 비용 발생 및 목록 조회 시 전체 스캔

그럼 LexoRank 알고리즘이 무엇이고 어떻게 이와 같은 한계를 극복할 수 있는지 설명하겠습니다.

LexoRank 알고리즘 소개

LexoRank는 "lexicographical rank"의 줄임말로 문자열의 사전적 순서를 활용해 순위를 결정하는 알고리즘입니다. 예를 들어, 일반적인 숫자 정렬에서 100은 99보다 낮은 순위이지만, LexoRank에서는 사전적 정렬에 따라 1이 9보다 앞에 있으므로 100이 99보다 높은 순위입니다.

그럼 LexoRank의 순위값은 어떻게 구성돼 있을까요?

LexoRank의 순위값 구조 및 작동 방법

LexoRank는 세 가지 주요 요소로 구성돼 있고, 각 요소에는 기존 랭킹 시스템의 한계를 극복하기 위한 명확한 역할이 부여돼 있습니다.

Bucket: 순위값 고갈 시 기존 순서를 유지하며 무중단으로 재조정하기 위한 요소
FixedKey: 모든 항목에 기본으로 부여돼 기본 순위로 사용되는 요소로, 항목 간에 빠르게 비교할 수 있는 고정 길이 키
VariableKey: FixedKey 고갈 시 할당되는 가변 길이 키

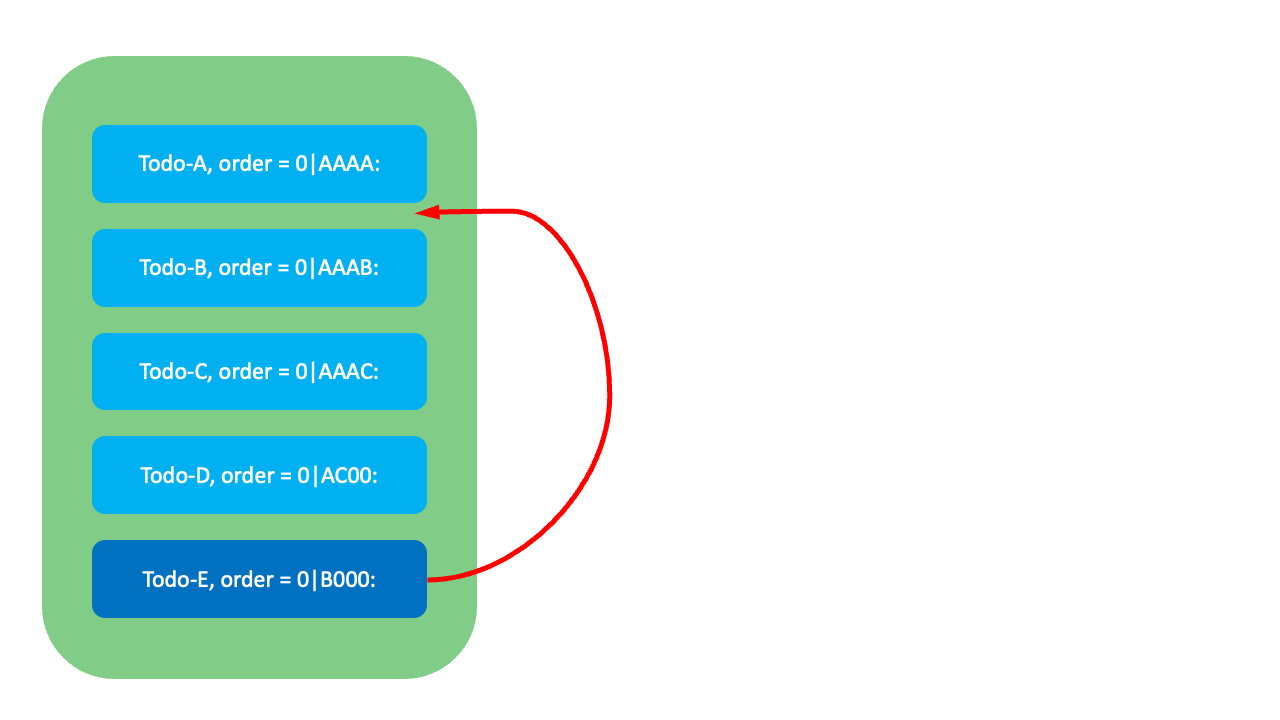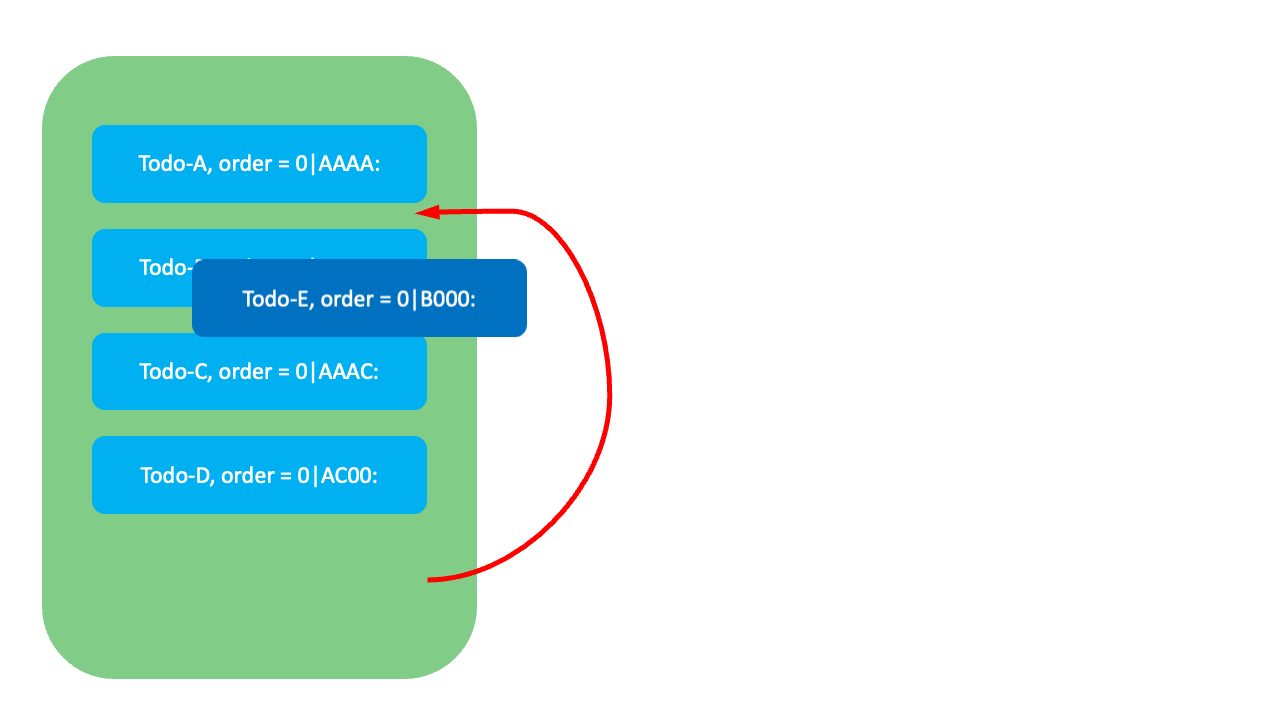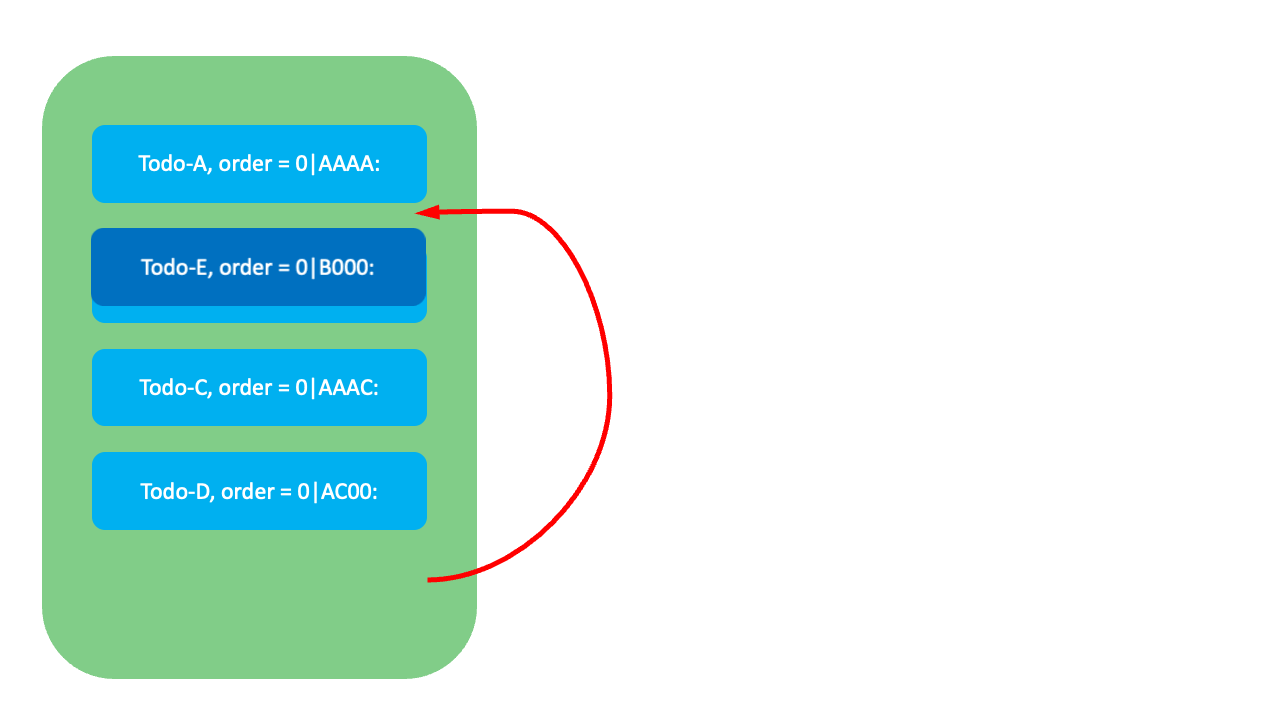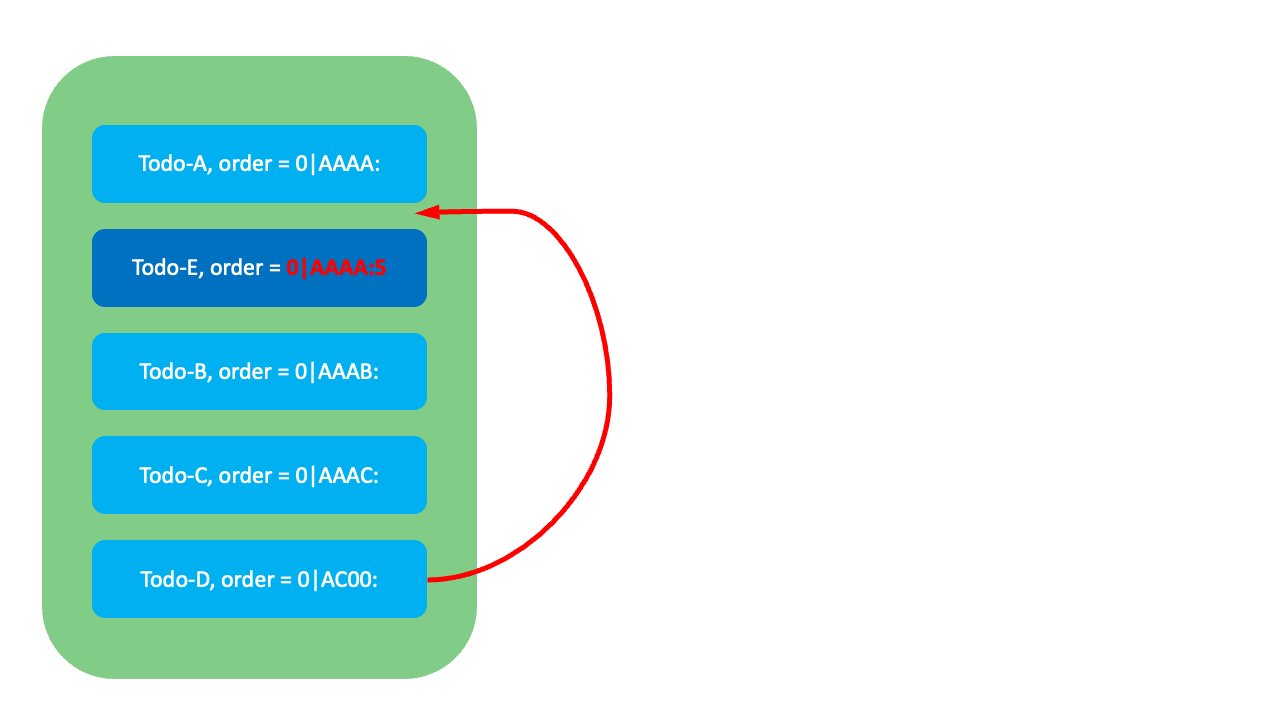
그럼 각 요소들이 어떻게 작동하는지 예시와 함께 살펴보겠습니다. 먼저 아래와 같이 Todo-A와 Todo-B 사이에 Todo-E를 삽입하려면 Todo-E에 Todo-A와 Todo-B 두 순위값의 중간에 해당하는 0|AAAB:를 FixedKey 값으로 할당합니다.

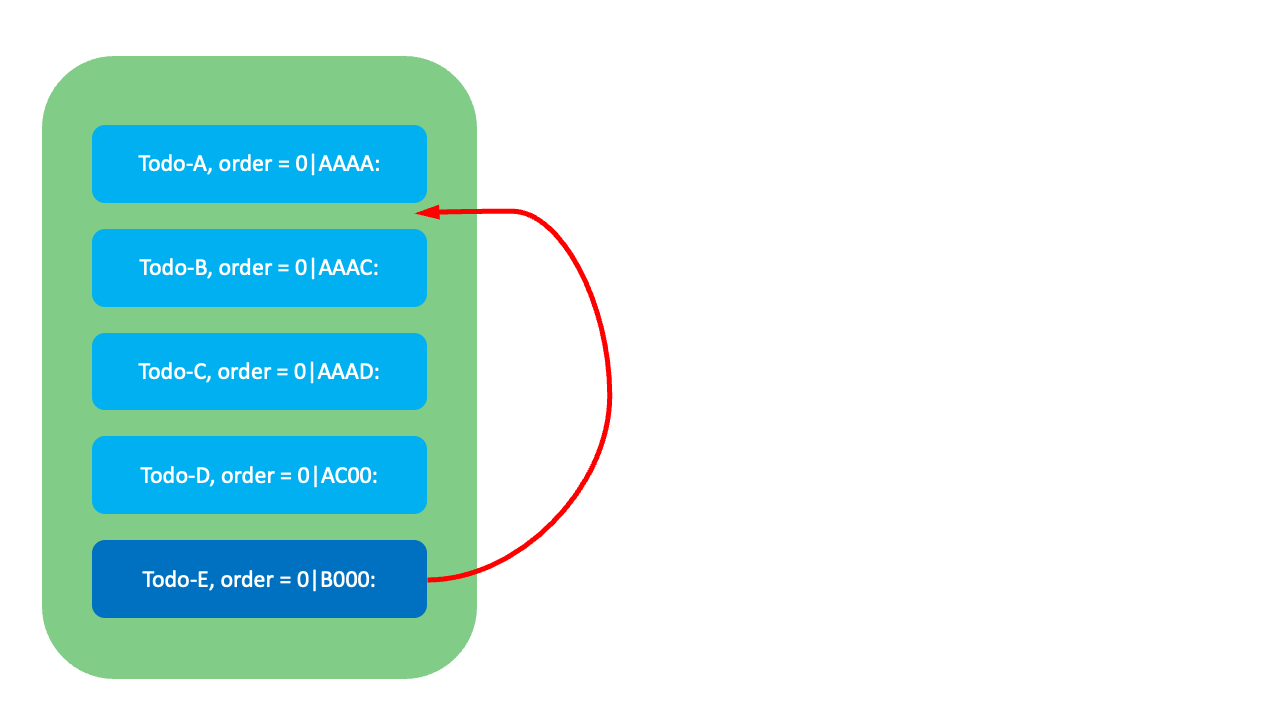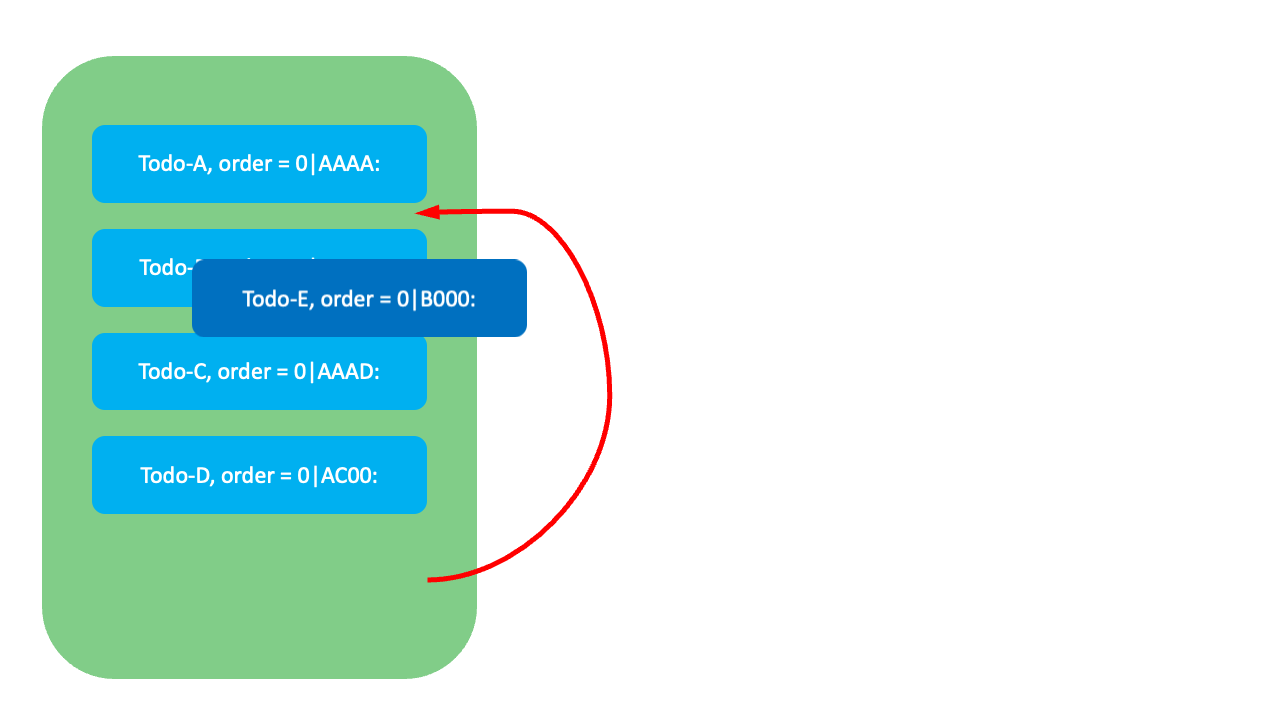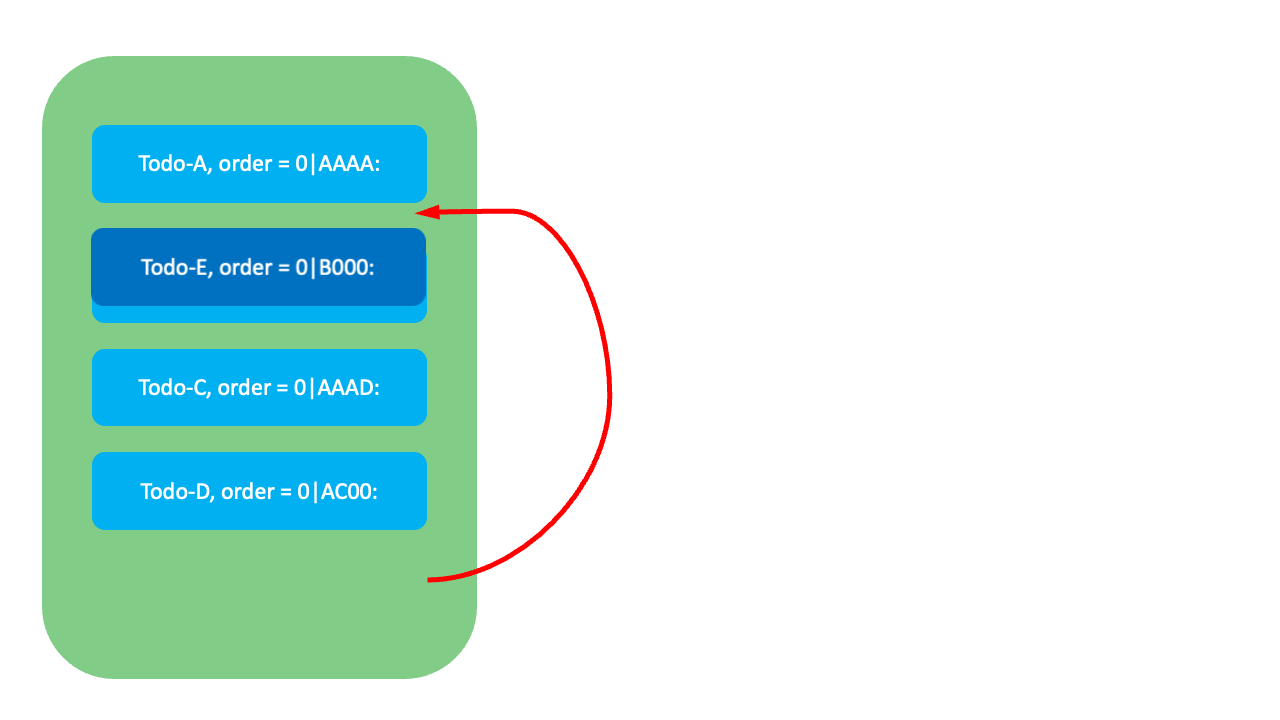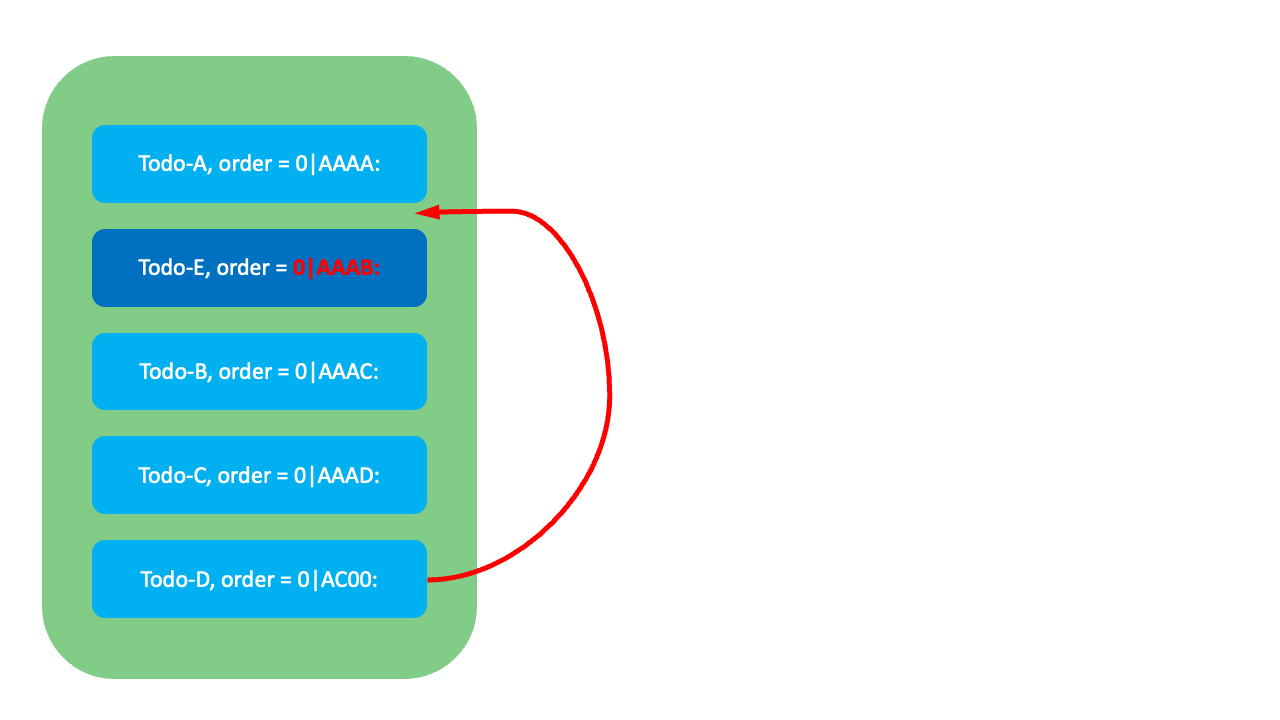
만약 Todo-A와 Todo-B 사이의 순위값이 고갈됐다면, Todo-A의 FixedKey(AAAA) 뒤에 규칙에 따라 VariableKey를 추가해 Todo-A의 뒤에, Todo-B의 앞에 오는 값을 할당합니다. 예를 들어 규칙에 따른 VariableKey가 5라면 0|AAAA:5가 할당됩니다. 이때 LexoRank는 FixedKey와 VariableKey를 조합해 대상 항목만 변경하므로 O(1)에 순서를 정렬할 수 있습니다.

이와 같이 VariableKey를 활용해 고갈을 지연시키기는 했지만 LexoRank 역시 언젠가는 순위값이 고갈되는 상황이 옵니다. 그렇다면 LexoRank는 어떻게 순위값 고갈을 사전에 감지하고 무중단으로 재조정할까요?

LexoRank가 순위값 고갈을 사전에 감지하는 방법

Atlassian이 공개한 문서에 따르면 순위값 고갈을 감지하는 방법은 아래와 같습니다.

순위값의 길이가 첫 번째 임계값인 128자에 도달하면 12시간 뒤 재조정 예약
예약된 12시간 동안 두 번째 임계값인 160자에 도달하면 즉시 재조정 수행
길이가 254자에 도달하거나 초과하면, 그 이상의 값을 생성하는 순위 작업은 중지

Jira는 위 기준을 이용해 순위값 고갈을 사전에 감지하며, 필요한 경우 적시에 재조정을 수행해 시스템 안정성을 유지합니다. 또한 사용자가 임계값에 도달한 상황이나 재조정 진행 상태를 쉽게 확인할 수 있도록 아래와 같은 대시보드를 제공합니다.

더불어 LexoRank 시스템의 무결성을 유지하기 위해 다음과 같은 항목을 지속적으로 확인합니다.

이제 고갈을 감지했을 때 어떻게 무중단으로 재조정하는지 설명하겠습니다.

LexoRank가 무중단으로 재조정하는 방법

LexoRank는 재조정이 필요할 때 세 개의 Bucket(0, 1, 2)을 순환하며 사용합니다. Bucket 증가 시(예: 0 → 1 또는 1 → 2)에는 아래 그림과 같이 낮은 순위의 순위값(0|DDD)부터 간격을 넓혀가며 다음 버킷으로 재할당합니다.

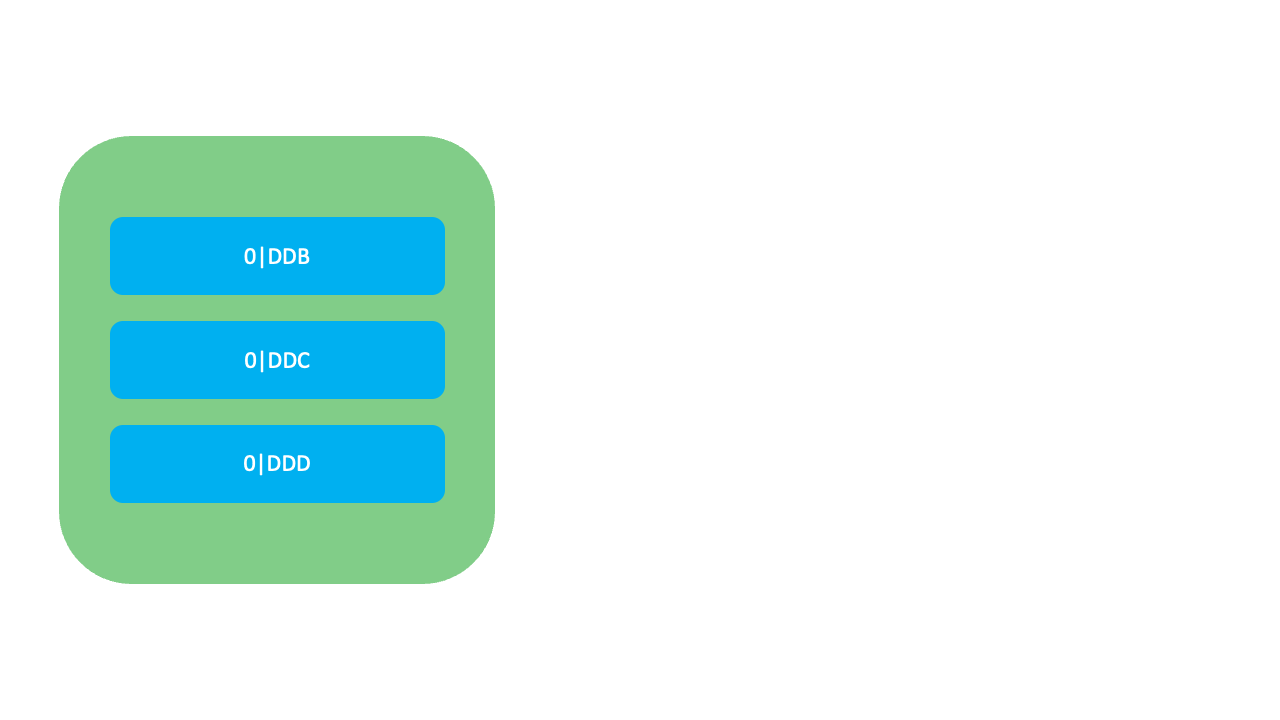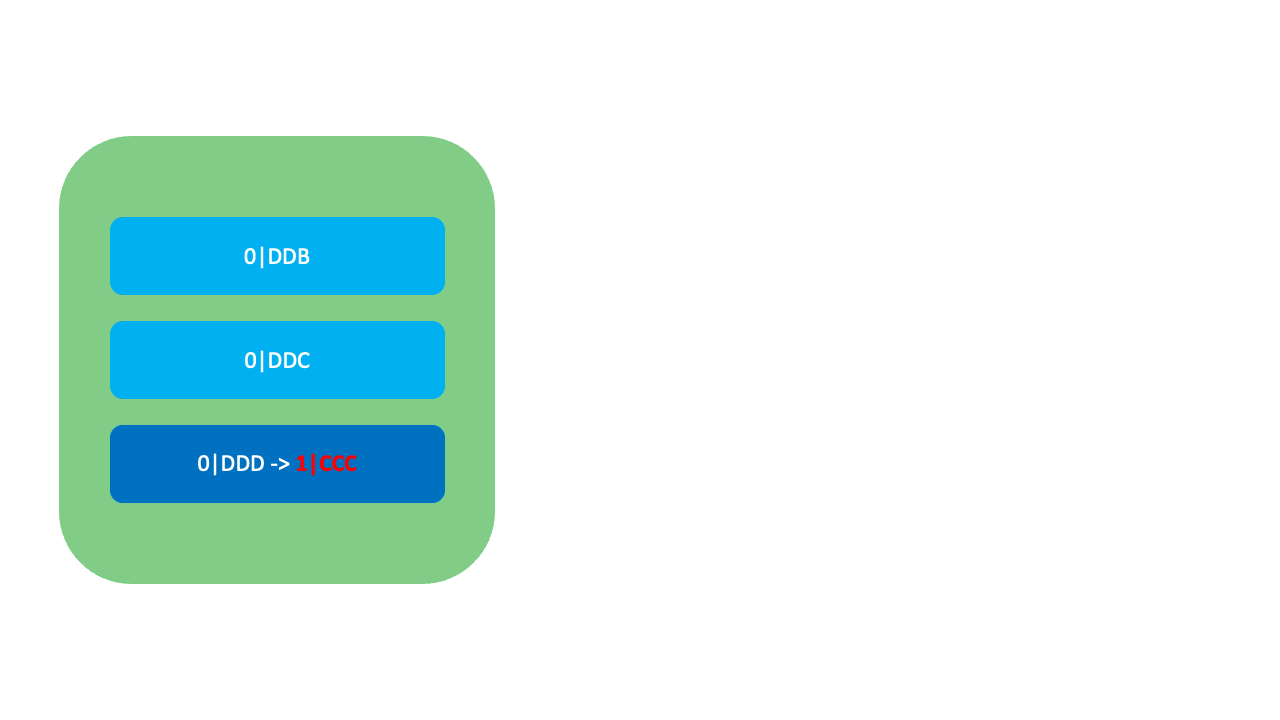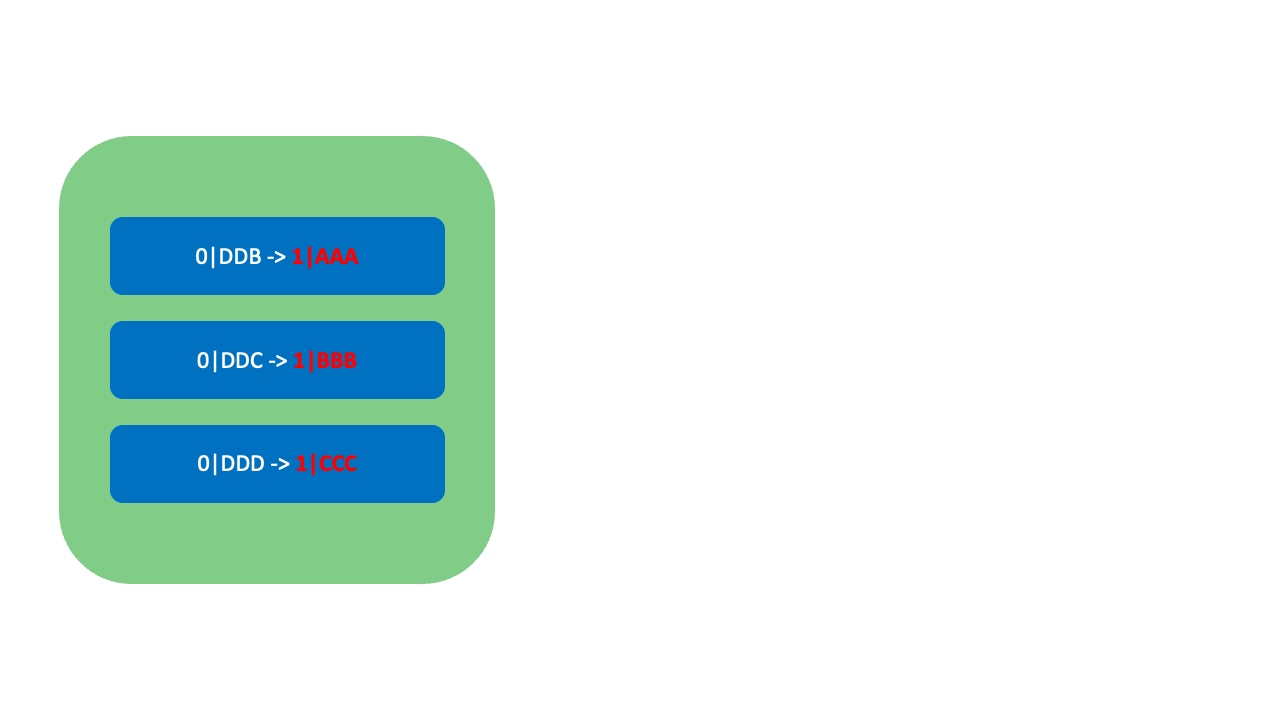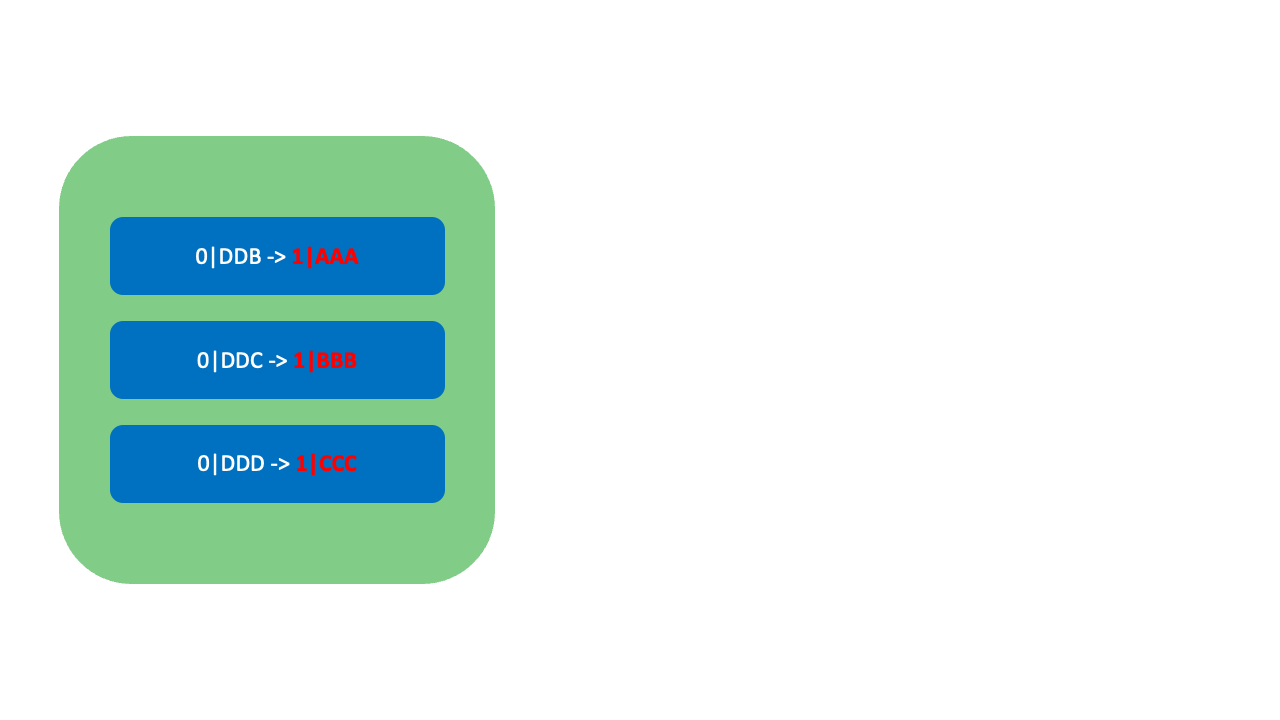현재 Bucket이 마지막 Bucket인 2일 경우 반대로 높은 순위의 순위값부터 간격을 넓혀가며 이전 Bucket인 0으로 재할당합니다. LexoRank는 이와 같이 Bucket을 통해 기존 순위를 유지하면서 무중단으로 순위값을 재조정할 수 있습니다. Bucket은 오로지 재조정에만 활용하며, 재조정 상황을 제외하고는 일반적으로 하나의 Bucket만 사용할 수 있습니다.

LexoRank의 특성 정리

앞서 설명한 내용을 바탕으로 기존 시스템의 한계를 LexoRank에서 어떻게 했는지 정리해 봤습니다.

기존 방식의 한계	LexoRank에서 극복한 방법
Integer 방식: 순서 변경 시 수정 범위가 큼(O(N))	문자열 순위값을 통해 수정 범위 축소(O(1))
GreenHopper 방식: 빠른 순위값 고갈 및 재조정 시 시스템 중단	무중단 재조정으로 순위값 고갈 방지
Linked List 방식: 순서 변경 시 2~4번의 고정 비용 발생 및 목록 조회 시 전체 스캔	인덱스 스캔으로 고정 비용 없이 빠른 조회

Tech Group에서 구현한 LexoRank 라이브러리 소개

이제 Tech Group에서 구현한 LexoRank 라이브러리를 소개하겠습니다. 저희는 앞서 소개한 LexoRank 알고리즘의 개념에 최대한 가깝게 구현하는 것을 목표로 설계를 시작했습니다. 먼저 라이브러리 구조를 간단히 살펴본 뒤, 구현 과정에서 마주한 이슈들과 각 이슈를 해결한 방법을 말씀드리겠습니다.

LexoRank 라이브러리 구조

저희는 LexoRank Key의 각 요소(Bucket, FixedKey, VariableKey)를 인터페이스로 정의하고, 사용자의 목적과 용도에 맞게 사용할 수 있도록 각 진수별로(10, 16, 36, 64) LexoDecimalRank와 LexoTimestampRank, 두 가지 구현체를 준비했습니다.

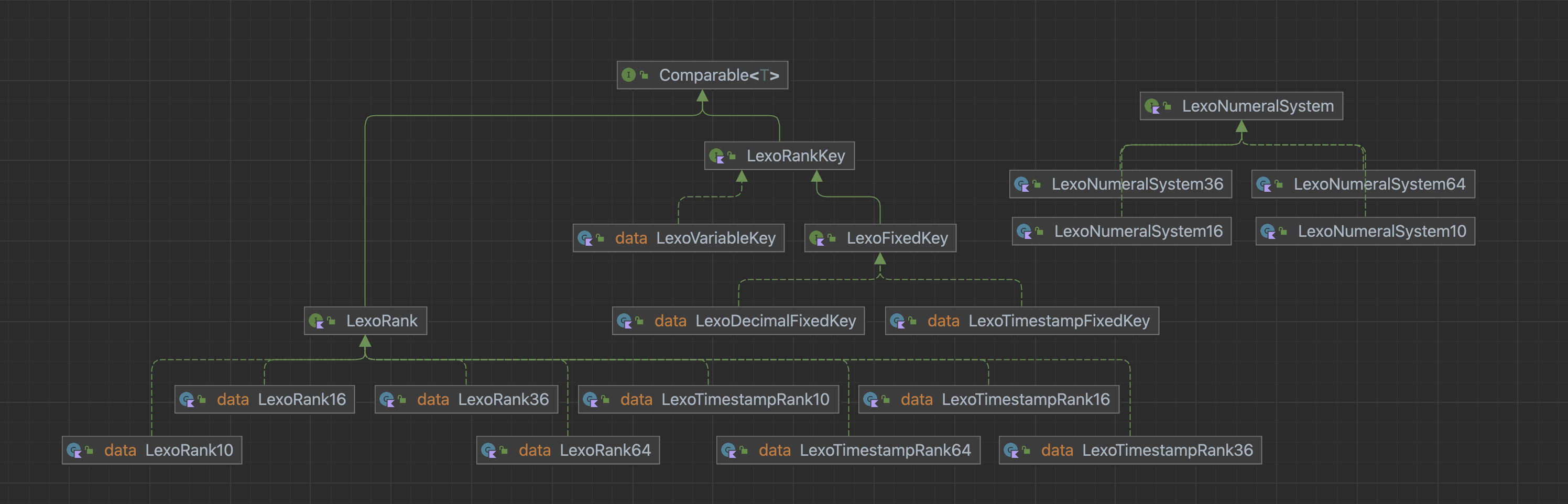
LexoDecimalRank	가장 마지막에 위치한 순위값 뒤에 새로운 순위값을 추가할 때, 순위값에 특정 갭(gap)을 더해 새로운 순위값을 생성하는 방식으로 일반적인 상황에서 사용할 수 있는 구현체입니다.
LexoTimestampRank	LexoDecimalRank와 달리 현재 타임스탬프의 UNIX 시간값을 순위값으로 사용해 생성하는 방식입니다. 동시 변경이 잦은 상황에서 순위값 충돌을 줄이고 싶을 때 사용할 수 있는 구현체입니다.

두 구현체의 차이점을 간단한 예시와 함께 설명하겠습니다.

아래와 같이 네 개의 항목이 있고 마지막 항목(Todo-D) 뒤에 세 명의 사용자가 동시에 새로운 항목을 생성한다고 가정해 봅시다. 이때 LexoDecimalRank를 사용하면 마지막 항목의 순위값(0|B000:)에 특정 갭(100)을 더해서 순위값을 생성합니다. 따라서 세 개의 항목이 모두 0|B100:이라는 같은 순위값을 반환받습니다. 이는 순위값의 고유성을 만족하지 못하기 때문에 결과적으로 재시도 비용이 발생합니다.

반면 LexoTimestampRank를 사용하면 현재 타임스탬프의 UNIX 시간값을 순위값으로 사용합니다. 따라서 밀리초 단위까지 구분되기 때문에 동일한 순위값이 반환될 확률이 극히 낮아집니다.

위 예시와 같이 동시에 여러 사용자가 접근하는 일이 빈번할 때에는 LexoTimestampRank를, 그렇지 않을 때는 항목 간 고정 간격이 보장되는 LexoDecimalRank를 사용할 수 있도록 두 가지 구현체를 제공합니다.

LexoRank 개발 중 발생한 이슈와 해결한 방법

LexoRank 개발 중 다음 세 가지 이슈가 발생했습니다.

FixedKey의 prev()와 next() 로직에 따른 가용 공간 고갈 이슈
VariableKey를 단순 중간값으로 처리 시 바로 최대 가변 길이에 도달하는 이슈
LexoTimestampRank 구현체를 사용해도 동일한 순위값이 생성되는 이슈

각 이슈를 소개하고 어떻게 해결했는지 말씀드리겠습니다.

FixedKey의 prev()와 next() 로직에 따른 가용 공간 고갈 이슈

항목 앞뒤로 새로운 순위값을 할당할 때, 간단하게 아래와 같은 방법을 떠올릴 수 있습니다.

prev(): (첫 번째 항목 키 + MIN) / 2
next(): (마지막 항목 키 + MAX) / 2

이 방식은 언뜻 보기에는 별문제가 없어 보이지만 자세히 살펴보면 항목이 추가될 때마다 가용 공간이 1/2로 줄어든다는 문제가 있습니다.

예를 들어, FixedKey 길이가 8이고 10진수를 사용하는 기준으로 극단적인 상황을 가정해 보겠습니다. 첫 항목 Todo-A가 중간 위치(0|50000000:)에 할당됐을 때 그 후로 계속 A 앞으로만 항목이 추가된다고 생각해 봅시다. 다음 항목은 A(0|50000000:)의 절반인 0|25000000:를 할당받습니다. 그다음 항목은 0|12500000:를 할당받습니다. 이와 같은 방식으로 몇 번 더 지속해 보면, 0|06250000 → 0|031250000: → .... → 0|00000001: 순서로 줄어듭니다. 이렇게 지속될 경우 25번만에 FixedKey가 고갈됩니다.

이 문제를 해결하기 위해 저희는 갭 개념을 도입해서, prev() 혹은 next()로 항목이 추가되더라도 간격을 보장하면서 동시에 FixedKey의 공간을 최대한 활용할 수 있도록 개발했습니다. 이때 갭의 크기는 서비스의 특성에 따라 커스터마이징할 수 있도록 구현했습니다.

override fun prev(): LexoRankKey {
	return if (gap > this) { // (현재 순위값 - 갭)이 음수인 경우 -> 일반적인 방식인 (현재 순위값 + MIN)/2 할당
 		val minKey = min(numeralSystem, keySize, gap = this.gap) // 최솟값을 가진 키 생성
		if (this == MIN) minKey else this.middle(minKey)
	} else {
		this.subtract(gap) // 현재 순위값에서 갭만큼을 뺀 값을 할당.
	}
}

VariableKey를 단순 중간값으로 처리 시 바로 최대 가변 길이에 도달하는 이슈

VariableKey는 가변 길이이지만, FixedKey와 같이 단순 중간값 연산으로 처리하면 바로 최대 길이에 도달해 저장 공간을 효율적으로 활용하지 못하는 이슈가 있었습니다.

VariableKey의 최대 길이가 8이라고 가정하고, FixedKey가 고갈된 상태에서 next()를 호출해 VariableKey를 사용하는 상황을 예시로 설명하겠습니다. 아래 왼쪽 그림을 보시면, FixedKey와 동일하게 최댓값(99999999)으로 중간값 연산을 하면 왼쪽 그림과 같이 VariableKey의 길이가 바로 5(1) → 74999999(8)로 증가합니다.

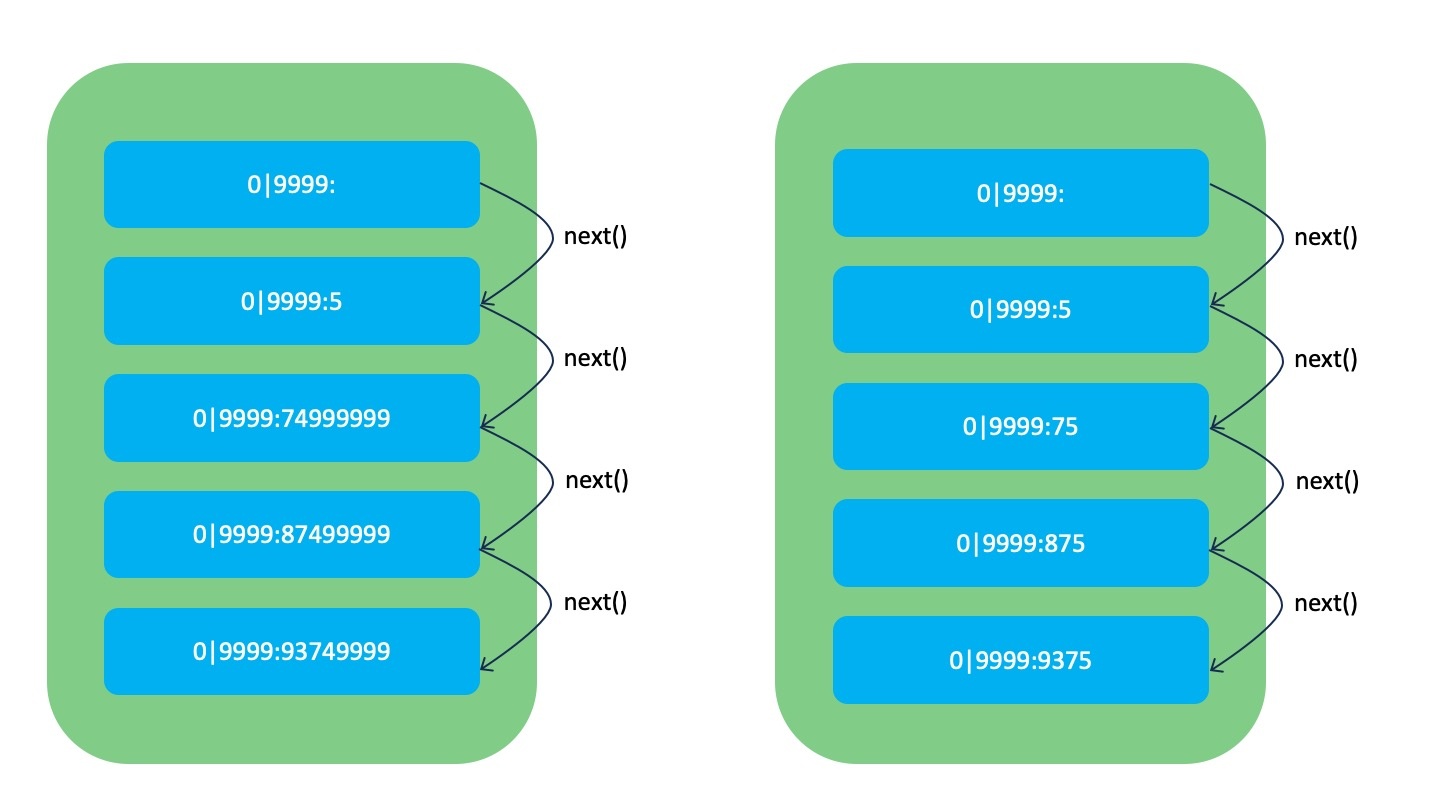
여기서 문제는 최댓값이 홀수라는 점입니다. 홀수에서 나누기 연산을 하므로 위 그림과 같이 next() 호출 두 번 만에 VariableKey가 최대 길이에 도달합니다. 이 때문에 저장 공간을 효율적으로 활용하지 못할 뿐 아니라 VariableKey 또한 빠르게 고갈됩니다.

저희는 이 문제를 해결하기 위해 기존 최댓값에 1을 더해 짝수로 만들어 위 오른쪽 그림과 같이 VariableKey의 길이를 최소화할 수 있도록 설계했습니다.

override fun next(): LexoVariableKey {
    return try {
        val maxKey = create(MAX_PLUS_ONE_VALUE, keySize + 1) // (MAX + 1 / keySize + 1)의 값을 가진 키 설정
        val result = create("0$value", keySize + 1).middle(maxKey) // keySize가 1 증가하므로 기존값 맨 앞에 0을 붙여서 middle() 호출

        result.value = result.value.drop(1)

        return create(result.value, keySize) // keySize를 다시 원래대로 유지한 채 결과값 키 반환
    } catch (e: RankExhaustedException) {
        if (value == MAX_VALUE) {
            throw e
        } else {
            create(MAX_VALUE, keySize)
        }
    }
}

LexoTimestampRank 구현체를 사용해도 동일한 순위값이 생성되는 이슈

앞서 LexoDecimalRank와 달리 LexoTimestampRank는 현재 시간을 기준으로 생성하기 때문에 동일한 순위값이 될 확률은 극히 낮다고 말씀드렸지만, 확률이 극히 낮을 뿐 아예 발생하지 않는 것은 아닙니다.예를 들어 한 번의 요청으로 N개 항목이 벌크 형태로 일괄 추가되는 상황을 생각해 볼 수 있습니다. 이때 처리 과정이 신속히 진행되면 여러 항목이 동일한 타임스탬프 값을 받게 될 가능성이 있습니다.

이런 상황을 피하기 위해 LexoTimestampRank에서도 이전 순위값과 같거나 작아지는 경우 갭 연산을 추가해 순위값을 할당하도록 개발했습니다.

현재 시간이 1714000000000이라고 가정하고, 다섯 개 항목을 동시에 추가할 때 아래와 같이 갭 연산을 추가해 순위값 할당 
# 첫 번째 항목: 1714000000000 
# 두 번째 항목: 1714000000100 
# 세 번째 항목: 1714000000200 
# 네 번째 항목: 1714000000300 
# 다섯 번째 항목: 1714000000400

마치며

LexoRank라는 개념을 처음 접한 뒤 이 개념을 실제 라이브러리로 개발하기까지 여러 번의 시행착오를 겪었습니다. 이슈를 해결하기 위해 로직을 세밀하게 조정하고 실제 사용 사례에 맞춰 성능을 튜닝하는 등의 작업을 수행해야 했는데요. 그 과정에서 LexoRank의 작동 원리를 더 깊이 이해할 수 있었습니다.

이 글이 효과적인 드래그 앤드 드롭 정렬 시스템을 구현하기 위해 고민하시는 많은 분들에게 한 줄기 빛과 같은 글이 되길 바랍니다. 저희가 겪은 고생이 반복되지 않도록 이 글을 널리 공유해 주시기 부탁드리며(🙂), 이만 마치겠습니다. 새해 복 많이 받으세요!

This work contains content adapted from the Atlassian Documentation Wiki at https://confluence.atlassian.com/