Journey to PQC: Protecting data in the quantum computing era

Hello, I'm Juhong Han from the Security R&D team. Our team is responsible for researching, developing, and consulting on various security technologies to enhance the overall security of LY Corporation services.

Currently, many IT services we use employ various encryption technologies to provide secure services. LY Corporation also utilizes cryptographic technologies in various areas to ensure that users can use our services with peace of mind—from end-to-end encryption like Letter Sealing and convenient user authentication through FIDO (Fast Identity Online) to building secure backup systems.

However, as research on quantum computers accelerates and their development becomes increasingly tangible, the security of the cryptographic technologies we currently trust may be compromised. To prepare for this, many experts are studying a field called post-quantum cryptography (PQC). In this post, we'll discuss how the development of quantum computers impacts current cryptographic systems and how we can protect our data in the quantum computing era.

Are modern cryptographic algorithms safe from the threat of quantum computers?

Quantum computing is a computing technology that processes data in a completely different way from traditional computers. While the computers we currently use represent data as 0s and 1s using bits, quantum computers use qubits, which can hold the states of 0 and 1 simultaneously. Thanks to this characteristic, quantum computers can process certain calculations much faster than conventional computers.

The key concepts of quantum computing are superposition and entanglement. A qubit in a superposition state can hold both 0 and 1 at the same time, producing an effect similar to performing parallel computations. Additionally, entangled qubits are strongly dependent on each other's states; when the state of one qubit is determined, the state of the other qubit is instantly determined as well. These properties of quantum computing allow quantum computers to solve specific problems like prime factorization very quickly.

According to the QUANTUM THREAT TIMELINE REPORT 2023 by Michele Mosca and Marco Piani, published under the Global Risk Institute license, about 27% of experts predict a more than 50% chance that a quantum computer capable of breaking 2048-bit RSA encryption within an hour could emerge in the next 10 years. When the timeframe extends to 30 years, around 78% of experts estimate a probability of over 70%.

Reference: QUANTUM THREAT TIMELINE REPORT 2023

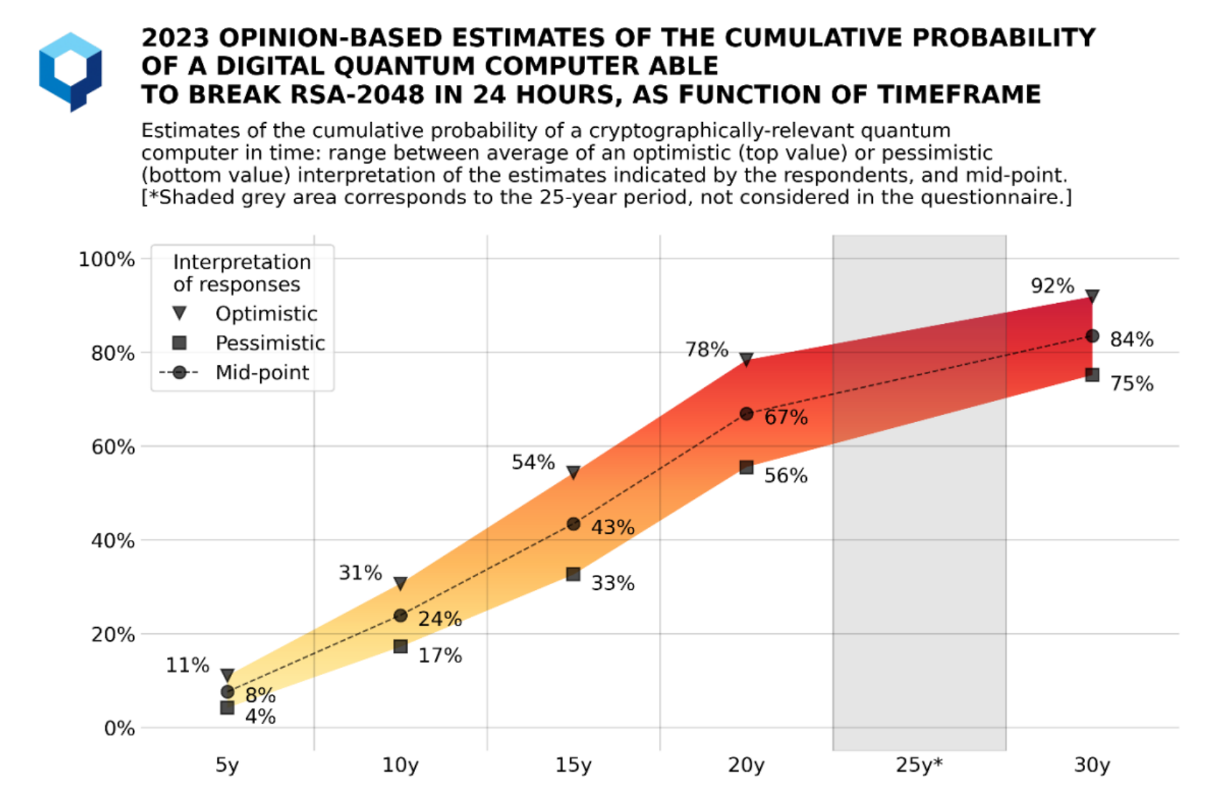
Although the development of quantum computers is still in its early stages, many experts believe that creating quantum computers capable of handling hundreds or even thousands of qubits is not far off. This expectation can be inferred from IBM's quantum computing development roadmap, as IBM is currently leading advancements in this field. The recently announced Heron processor by IBM is designed to stably handle 133 qubits and features a modular architecture that allows for flexible scalability. While the current limit is expanding up to 399 qubits using three processors, IBM aims to handle up to 2,000 qubits per processor after 2033. If these processors are configured modularly, we might indeed be able to utilize thousands or even tens of thousands of qubits.

Then, if quantum computers capable of handling tens of thousands of qubits are developed in the future, what impact will that have on modern cryptographic systems?

Symmetric key cryptography and hash functions

Symmetric key cryptography is an algorithm that uses the same key to encrypt and decrypt data. It is generally fast and efficient, making it suitable for processing large data blocks. Because of these advantages, most general data encryption relies on symmetric key cryptography.

In symmetric key cryptography, security is typically determined by the length of the key. For instance, an algorithm that uses a 128-bit key has a security strength of 128 bits. Here, security strength refers to the number of operations required to find the encryption key. For example, a 128-bit security strength means that it would take $2^{128}$ operations to find the key. Given current computational capabilities, performing $2^{128}$ operations would take more than 10 trillion years, making it infeasible to break within a practical timeframe.

However, such symmetric key cryptography can be broken by Grover's algorithm. Grover's algorithm is a quantum algorithm that operates on quantum computers and can significantly reduces the time required to solve non-linear search problems from $O(N)$ to $O(\sqrt{N})$ , which has a greatly impacting the security of symmetric key cryptography and hash functions.

For example, if Grover's algorithm is used to attack symmetric key cryptography, the security strength is halved, meaning that the security of a 128-bit symmetric key encryption algorithm is reduced to 64 bits. This reduction shortens the time required for an attack from over 10 trillion years to approximately six months.

The situation is similar for hash functions. A hash function converts data into a fixed-length output that looks like a random string of bits. Hash functions are designed so that even a one-bit difference in the input produces a completely different output. So, they are primarily used for verifying data integrity and are very difficult to forge due to their design.

In general, for an $N$ -bit hash, it is known that finding the preimage (the original data corresponding to a given hash value) requires $2^N$ computations, and finding a collision pair (two different inputs producing the same hash value) requires $2^{\frac{N}{2}}$ computations.

However, using Grover's algorithm, these problems can be solved with only $2^{\frac{N}{2}}$ and $2^{\frac{N}{3}}$ computations, respectively.

Asymmetric key cryptography

Asymmetric key cryptography, also known as public key cryptography, is an algorithm that uses different keys for data encryption/decryption and signature generation/verification. One key is a public key that anyone can access, while the other is a private key accessible only to the owner. Notable asymmetric key algorithms include RSA (Rivest-Shamir-Adleman) from the Integer Factorization Cryptography (IFC) family, and ECDSA (Elliptic Curve Digital Signature Algorithm) and ECDH (Elliptic-curve Diffie-Hellman) from the Elliptic Curve Cryptography (ECC) family.

Unlike symmetric key cryptography and hash functions, the security of modern public key cryptography algorithms is based on mathematical problems that are difficult to solve. Therefore, their security is guaranteed under the assumption that no efficient algorithm exists to solve these mathematical problems.

However, such asymmetric key cryptography can be broken by Shor's algorithm. Shor's algorithm is a quantum algorithm that operates on quantum computers and can solve the underlying problems of RSA and ECC-based cryptosystems in a short time. For example, RSA is designed based on the difficulty of factoring large numbers; while it would take current computers trillions of years to factor a 2048-bit key, using Shor's algorithm, this task can be accomplished in a very short time (approximately 8 hours using a quantum computer with about 20 million qubits according to the article: How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits).

How to prepare for the threat of quantum computers

Symmetric key and asymmetric key algorithms are widely used across various IT systems, including financial services, and are crucial for protecting data. Therefore, it is essential to prepare for potential security threats posed by quantum algorithms. Let’s explore how we can protect our data against these quantum threats. Below is a table summarizing the quantum algorithms that pose a threat to each type of encryption method and the corresponding countermeasures.

Category	Quantum algorithm	Countermeasure	Before	After
Symmetric Key	Grover's Algorithm	Increase Key Length	128, 192, 256	At least 256
Hash	Grover's Algorithm	Increase Output Length	224, 256, 384, 512	At least 384, 512
Asymmetric Key	Shor's Algorithm	Replace Algorithm	IFC, ECC, FFC	Lattice, Code, Isogeny, Hash, Multivariate

Fortunately, addressing this issue in symmetric key cryptography is not particularly difficult. Most of the current symmetric key cryptographic algorithms support up to 256-bit keys, so for systems using 128-bit or 192-bit keys, the key length can be increased to 256 bits. And, hash functions can be replaced with algorithms that have longer outputs lengths, ensuring security strength of 128 bits or more. Of course, replacing algorithms in already deployed systems may not be easy, but since there are algorithms whose security has been sufficiently proven, there's no need to develop new ones.

However, asymmetric key cryptography cannot be protected simply by reusing existing algorithms like symmetric key cryptography or hash functions. Since the underlying problems used in algorithm design are compromised, we need to create algorithms based on new mathmatical problems that are difficult to solve even with quantum algorithms. Consequently, many experts are currently researching Post-Quantum Cryptography (PQC) to prepare for this challenge.

PQC standardization and transition

CRQC (Cryptographically Relevant Quantum Computer) is a term used by the NSA (National Security Agency) to refer to a quantum computer capable of attacking actual cryptographic systems. PQC refers to algorithms that are secure even against attacks from CRQCs, which is why it's also called Quantum-Resistant Cryptography. The PQC category can include symmetric key cryptography with extended key lengths and hash functions with longer output lengths. However, it generally refers to algorithms based on mathematical problems that are difficult to solve in both classical and quantum environments, often used to replace existing public key cryptosystems.

Status of PQC Algorithm Standardization

In 2017, the National Institute of Standards and Technology (NIST) in the United States initiated a PQC competition aimed at standardizing cryptographic algorithms that remain secure even against attacks from cryptographically relevant quantum computers (CRQCs). In response, experts from around the world submitted algorithms based on diverse mathematical foundations. These algorithms were evaluated on various criteria, including security, performance in existing computing environments, ease of replacement, perfect forward secrecy, resistance to side-channel attacks, and robustness against misuse.

Reference: NIST PQC: LOOKING INTO THE FUTURE

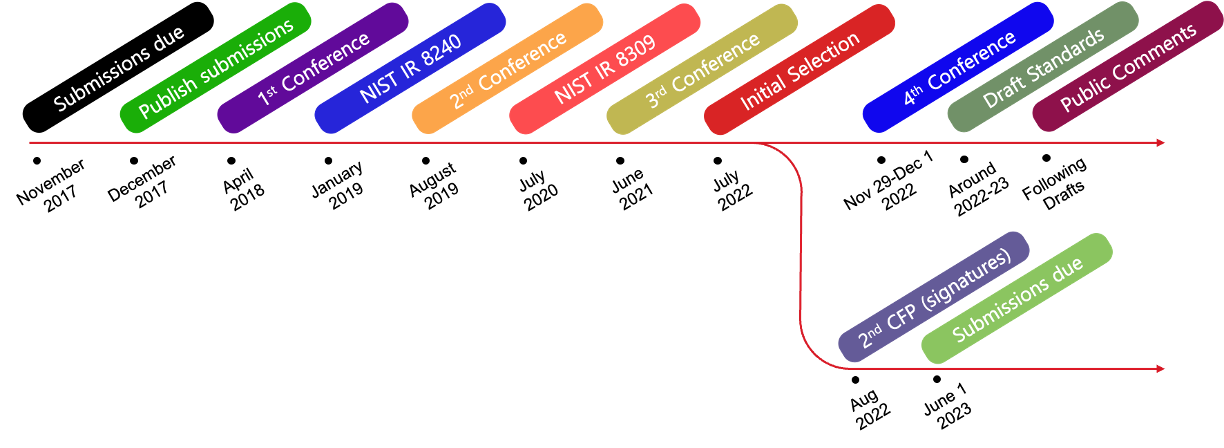
A total of 69 algorithms were submitted to the PQC competition, and over several years of evaluation processes, many algorithms were eliminated. After three rounds, in July 2022, the following four algorithms were selected as the final candidates for standardization. In 2024, they were officially approved as Federal Information Processing Standards (FIPS).

CRYSTALS-Kyber(ML-KEM): Lattice-based asymmetric encryption and key encapsulation algorithm
CRYSTALS-Dilithium(ML-DSA): Lattice-based digital signature algorithm
FALCON(FN-DSA): Lattice-based digital signature algorithm
SPHINCS+(SLH-DSA) : Hash-based signature algorithm

However, since the only selected KEM algorithm was lattice-based, NIST is conducting a fourth round with other KEM algorithms—BIKE, Classic McEliece, HQC, and SIKE—that are based on different mathematical foundations. This is to prepare for potential vulnerabilities in lattice-based cryptography. Additionally, because no signature algorithms were included in the fourth round, an extra round focusing on signature algorithms is also being carried out.

Threat models and timing of transition

Many experts assert that we should start preparing for the transition to Post-Quantum Cryptography (PQC) now. Although the development of CRQCs is still some way off, some readers might wonder why we need to research PQC and prepare for migration already. This can be explained by the HNDL attack and Mosca's theorem.

The Harvest Now, Decrypt Later (HNDL) attack involves collecting and storing data now with the intention of decrypting it later when attacks using CRQCs become possible. Such attacks can affect sensitive data that needs long-term security or long-lived data like signatures used in firmware and software. Therefore, even if quantum attacks are not yet practically feasible, there is a need to develop and deploy cryptographic algorithms in advance to against them.

So, when should we start the transition to PQC? We can roughly estimate the timing using Mosca's Theorem, which considers three main variables.

$x$ : The amount of time the security of current cryptographic algorithms needs to be maintained
$y$ : The time required to design, standardize, deploy, and migrate to PQC algorithms
$z$ : The time remaining until quantum computers become powerful enough to break current cryptographic algorithms

To be safe from the threat of CRQCs, the following inequality must be satisfied:

$x + y < z$

In other words, the sum of the time required to develop and migrate to PQC algorithms ( $y$ ) and the period during which current cryptographic algorithms remain secure ( $x$ ) must be shorter than the time remaining until CRQCs are developed ( $z$ ).

Currently, many experts estimate that even with a conservative assumption about the development speed of quantum computers, CRQCs will emerge around 2030 due to rapid advancements in science and technology. Based on this estimate, considering the point when PQC algorithms began to be actively researched, $z$ can be thought of as approximately 20 years.

So, how long does the migration corresponding to $y$ take?

Migration tasks in IT environments often require more time than anticipated because the factors to consider vary depending on the operational environment, and some environments may take several years until the next deployment. Therefore, more time is needed than one might think. This can be confirmed through other past transition cases. For instance, it took approximately 10 years after standardization for SHA-2 and AES to be applied to most systems, and similarly, it took over 10 years to transition to TLS 1.2.

The dates marked with a hammer indicate when practical attacks on each algorithm were successful.

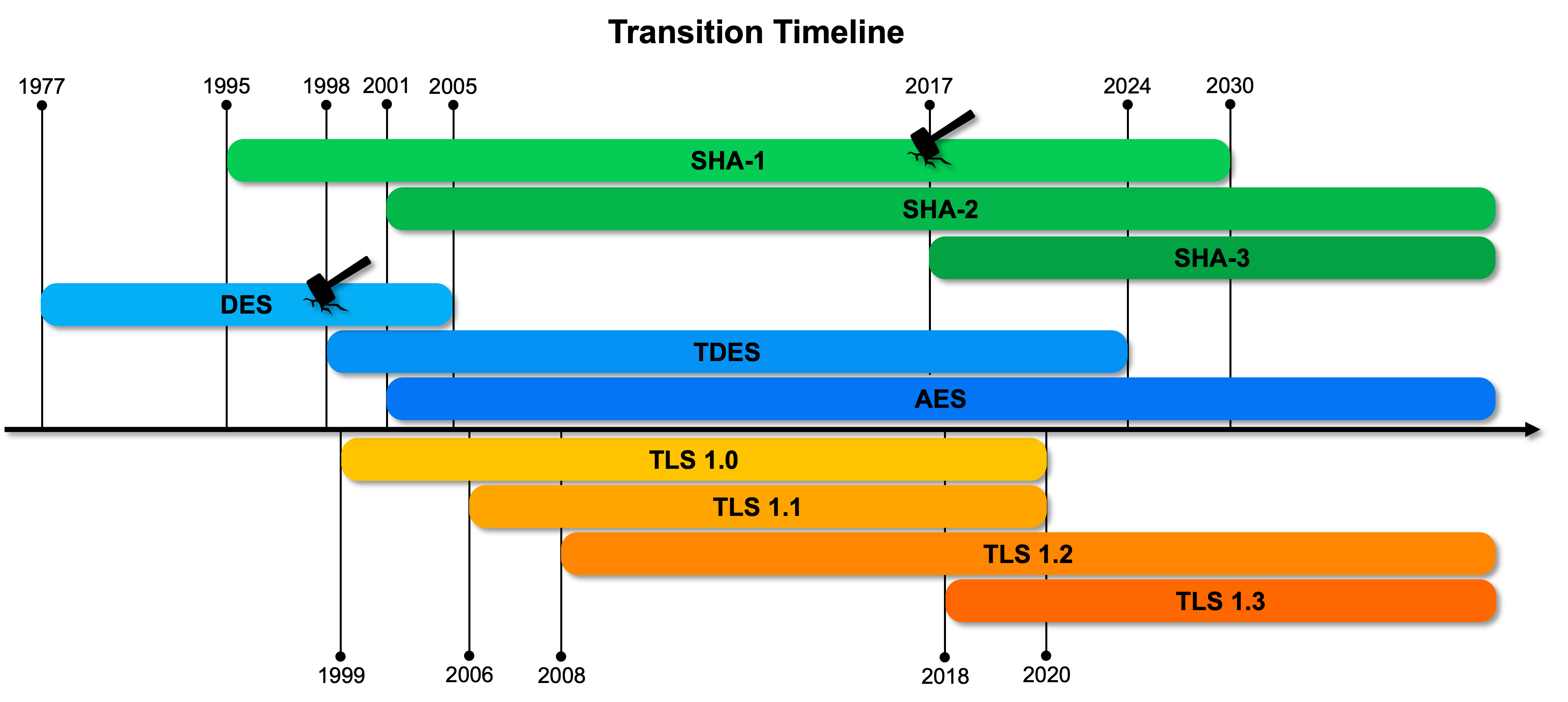
Because the process of transitioning to PQC is expected to be more complex and extensive than previous migration efforts, we can consider the time required for migration $y$ to be at least 10 years or more. Therefore, based on the above assumptions, we realize the necessity of starting migration preparations now.

In fact, these assumptions are reflected in the PQC transition roadmaps of various countries. The U.S. NSA has announced CNSA 2.0 (Commercial National Security Algorithm Suite 2.0), which includes PQC algorithms. According to the roadmap released at that time, the goal is to start preparations in most sectors from 2024 and complete the transition by 2033. In alignment with this roadmap, the White House (reference) and major agencies are issuing new policies and regulations. Similarly, Germany's BSI (reference), the UK's NCSC (reference), France's ANSSI (reference), and Canada's CSE (reference) have each published PQC transition roadmaps and guidelines for both the public and private sectors.

Reference: Announcing the Commercial National Security Algorithm Suite 2.0

Preparing for the Transition to PQC: Hybrid Mode

So, how should we prepare for the transition to Post-Quantum Cryptography (PQC)? While experts have various opinions on the PQC transition process, a phased transition using hybrid modes is currently widely adopted [References: 1, 2, 3, 4, 5, 6].

A hybrid mode involves using existing asymmetric key cryptographic algorithms and PQC algorithms simultaneously. The main reason experts opt for hybrid modes instead of solely relying on PQC is to protect against potential unknown vulnerabilities in the newly proposed PQC algorithms. Since these PQC algorithms are relatively new technologies that haven't been researched for a long time, there's a possibility of theoretical flaws or undiscovered vulnerabilities in current systems. Therefore, by choosing a hybrid structure, we ensure that even if new vulnerabilities are found during the PQC transition, we can still be protected through existing cryptographic algorithms. Selecting the hybrid mode allows for a gradual transition until PQC algorithms are fully verified and stabilized, and even if new vulnerabilities are discovered, the existing cryptographic algorithms act as a hedge, minimizing security risks.

In fact, the algorithm Rainbow, which was submitted to the NIST PQC competition and was a finalist in the third round, was eliminated after a new key recovery attack was announced (reference). Similarly, a vulnerability was discovered in the SIKE algorithm, which had been experimentally implemented in Google Chrome in the past (reference); however, thanks to the adoption of a hybrid structure, it did not lead to a security incident.

Moreover, the hybrid mode has the advantage of being configured by adding PQC algorithms to existing specifications. This makes it relatively easy to satisfy availability in existing product protocols and comply with various regulatory requirements. As such, it is currently being evaluated and adopted as the most effective method to prepare for the transition at this point in time.

Of course, there are risks associated with the hybrid mode. Since the hybrid structure uses two cryptographic algorithms simultaneously, not only does the design and implementation become more complex, but additional issues like interoperability problems and more complicated key management can arise, potentially leading to unforeseen security vulnerabilities. Moreover, because the hybrid structure is a temporary solution, we will eventually need to transition to a PQC-only structure once the security of PQC has been sufficiently verified. As seen in past cases like AES and SHA-2, such transition processes are complex tasks that require significant time and cost. Therefore, while the hybrid mode is an important strategy for maintaining current security systems while preparing for the threat of quantum computers, it's important to remember that it is not a long-term solution.

Conclusion

In this article, we examined how the advent of quantum computers threatens the security of modern cryptographic systems and explored the reasons and methods for preparing for this situation. As previously mentioned, while symmetric key cryptography and hash functions can be addressed relatively easily, asymmetric key cryptography requires considerable time to develop and implement new algorithms. Therefore, we need to prepare for the transition of asymmetric key cryptography in stages through temporary solutions like hybrid modes.

As shown in the PQC transition roadmaps announced by governments and security agencies worldwide, the next 10 to 20 years will be crucial for preparing and implementing the shift to post-quantum cryptography (PQC). With ongoing research in quantum computing and PQC, many advancements and changes are anticipated. Therefore, to continuously protect our data, it is essential to adapt swiftly to these changes.

We hope this blog has enhanced your understanding of cryptographic technology and security in the era of quantum computing. In our next post, we will explore the efforts LY Corporation is making to support the transition to PQC. We appreciate your interest and thank you for taking the time to read this post.